Medical Statistics Formulas and Equations
|
Note: In the formulas the symbol \( \ln(x) \) is the natural logarithm. In other words the inverse function of \( \text{e}^x = \exp(x) \) meaning
that \( \ln(\text{e}^x) = x \) and that \( \text{e}^{\ln(x)} = x \).
In some text books, \( \ln(x) \) is written as \( \log(x)\). The expression \( \log(x) \) is, however, normally attributed to the base-10-logarithm, not
the natural logarithm.
Content Menu: (click here to hide)( ↓ click the big red headlines to show/hide content ↓ ) Risk and Odds
Calculate proportions, their confidence intervals plus test equality between proportions HERE.
Calculate risk, odds, risk ratio, odds ratio and confidence intervals plus perform test HERE. Proportions:
Proportion: $$ \widehat{p} = \frac{e}{n} $$or (as a percentage): $$ \widehat{p} = \frac{e}{n} \cdot 100 $$Standard error of proportion: $$ SE(\widehat{p})=\sqrt{\frac{\widehat{p} \cdot (1-\widehat{p})}{n}} $$Approximated 95 % CI of proportion: $$ 95\% \; CI=[\widehat{p} - 1.96 \cdot SE(\widehat{p}) \; : \; \widehat{p} + 1.96 \cdot SE(\widehat{p})] $$Exact 95 % CI of proportion: $$ 95\% \; CI=\left[\frac{e}{e + (n - e + 1) \cdot f_1} \; : \; \frac{e + 1}{e + 1 + \frac{n - e}{f_2}}\right] $$where f1 is the 0.975 quantile of the f-distribution with the degrees of freedom DF1 = 2(n - e) + 2 and DF2 = 2e. The number f2 is the 0.975 quantile of the f-distribution with degrees of freedom DF1 = 2e + 2 and DF2 = 2(n - e). Odds: to find the odds from a given risk (or vice versa), you can use the following formulas to convert from odds to risk and from risk to odds; $$ risk=\frac{odds}{1+odds} \; \iff \; odds=\frac{risk}{1-risk} \;\;\; $$and as a consequence (dealing with proportions): $$ \widehat{p}=\frac{odds}{1+odds} \; \iff \; odds=\frac{\widehat{p}}{1-\widehat{p}} $$Standard Error of the logarithmic transformed odds: $$ SE\left({\ln(odds)}\right)=\sqrt{\frac{\;\;\; 1 \;\;\;}{e} + \frac{ 1 }{\; n-e \;}} $$Approximated 95 % CI of ln(odds): $$ 95 \; \% \; CI=[\ln\left({odds}\right) - 1.96 \cdot SE\left({\ln(odds)}\right)\;\; : \;\; \ln\left({odds}\right) + 1.96 \cdot SE\left({\ln(odds)}\right)] $$Approximated 95 % CI of odds: $$ 95\; \% \;CI = [\text{e}^{\ln\left({odds}\right) - 1.96 \cdot SE\left({\ln(odds)}\right)}\;\; : \;\; \text{e}^{\ln\left({odds}\right) + 1.96 \cdot SE\left({\ln(odds)}\right)}]$$ $$ =\; [\exp\left({\ln\left({odds}\right) - 1.96 \cdot SE\left({\ln(odds)}\right)}\right) \;\; : \;\; \exp\left({ \ln\left({odds}\right) + 1.96 \cdot SE\left({\ln(odds)}\right) }\right)] $$or (alternatively): $$ 95 \; \% \; CI = \left[\frac{odds}{\text{e}^{1.96 \cdot SE\left({\ln(odds)}\right)}} \;\; : \;\; odds \cdot \text{e}^{1.96 \cdot SE\left({\ln(odds)}\right)} \right] $$Exact 95 % CI of odds: To calculate the exact 95 % confidence interval of a given odds, one could calculate an exact 95% CI of the proportion using the f-distribution (see above) and then convert both the lower and upper bound in that interval to odds via the formula: $$ odds = \frac{proportion}{1 - proportion}$$Risk:
The risk of an event occurring is the probability that the event happens given that another event has already happened. In this case, for example: Either the risk of getting the outcome (D) given the fact that one has been exposed (E). Or the risk of getting the outcome given not exposed (not E). $$ Risk_1 = P(D \: | \: E) = \frac{d_1}{n_1} $$ $$ Risk_2 = P(D \: | \: not \: E) = \frac{d_2}{n_2} $$Standard Error of risk: $$ SE(risk_1)=\sqrt{\frac{risk_1 \cdot (1-risk_1)}{n_1}} , SE(risk_2)=\sqrt{\frac{risk_2 \cdot (1-risk_2)}{n_2}} $$95 % Confidence Interval of risk: $$ 95\; \% \;CI = \left[ lower \: bound \: : \: upper \: bound \right] $$ $$ = \left[ risk - 1.96 \cdot SE(risk) \; : \;risk + 1.96 \cdot SE(risk) \right] $$If you need to find the Standard Error knowing only the 95 % Confidence Interval : $$ SE(risk) = \frac{upper \: bound - lower \: bound}{2 \cdot 1.96} = \frac{upper \: bound - lower \: bound}{3.92} $$Risk Difference$$ RD = risk_1 - risk_2 $$ Standard error of Risk Difference: $$ SE(RD)=\sqrt{SE(risk_1)^2+SE(risk_2)^2} $$95 % Confidence Interval of RD: $$ 95\; \% \; CI = \left[ RD - 1.96 \cdot SE(RD) : RD + 1.96 \cdot SE(RD) \right] $$Calculation of z-value of RD in the general case, null hypothesis is denounced H0: $$ z = \frac{| RD- H0 |}{SE(RD)} $$In the standard case where H0 = 0: $$ z = \frac{| RD- 0 |}{SE(RD)} = \frac{| RD |}{SE(RD)} $$p-value of RD corresponding to a given z-value: (because the normal distribution is two-sided): $$ p=2 \cdot \int_z^{\infty} \frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2} \cdot x^2} dx $$i.e. two times the area under the bell-shaped normal distribution curve from z to infinity Risk Ratio (or: Relative Risk or: Prevalence Rate Ratio)$$ RR=\frac{Risk_1}{Risk_2} = \frac{P(D \: | \: E)}{P(D \: | \: not \: E)} = \frac{\frac{d_1}{n_1}}{\frac{d_2}{n_2}}=\frac{d_1 \cdot n_2}{n_1 \cdot d_2} $$ If the number RR is greater than 1 it is a worsening factor to be exposed to the exposure compared to being not exposed (because then the risk of getting outcome in the exposed group is greater than the risk in the non exposed group). If RR is between 0 and 1 it is an bettering factor being exposed compared to being not exposed. Standard Error of the logarithmic transformed RR, ln(RR): $$ SE(\ln\left({RR}\right)) = \sqrt{\frac{1}{d_1} - \frac{1}{n_1} + \frac{1}{d_2} - \frac{1}{n_2}} $$95 % Confidence Interval of ln(RR): $$ 95 \; \% \; CI = \left[\ln\left({RR}\right) - 1.96 \cdot SE(\ln\left({RR}\right)) : \ln\left({RR}\right) + 1.96 \cdot SE(\ln\left({RR}\right))\right] $$95 % Confidence Interval of RR: $$ 95 \; \% \; CI = \left[ e^{\ln\left({RR}\right) - 1.96 \cdot SE(\ln\left({RR}\right))} : e^{\ln\left({RR}\right) + 1.96 \cdot SE(\ln\left({RR}\right))} \right] $$If this interval contains 1 (i.e. lower bound is negative and upper bound is positive) then we cannot reject the H0 hypothesis saying that RR = 1 (on a 5% significance level). In other words; then the two risks wouldn't be significantly different from each other. In this case the p-value from the test will be above 0.05. The p-value will be below 0.05 if the interval doesn't contain 1. In these cases it is therefore not strictly necessary to perform the z-test, a look at the confidence interval will suffice. or, (alternatively): $$ 95 \; \% \; CI = \left[\frac{RR}{e^{1.96 \cdot SE(\ln\left({RR}\right))}} : RR \cdot e^{1.96 \cdot SE(\ln\left({RR}\right))} \right] $$If you need to find the SE(ln(RR)) knowing only the 95 % Confidence Interval : $$ SE(\ln(RR)) = \frac{\ln(upper \: bound) - \ln(lower \: bound)}{2 \cdot 1.96} $$ $$ = \frac{\ln(upper \: bound) - \ln(lower \: bound)}{3.92} $$Calculation of z-value in the general case, where the null hypothesis is H0: $$ z = \frac{| \ln\left({RR}\right) - \ln\left({H0}\right)|}{SE(\ln\left({RR}\right))} $$In the standard case where H0 = 1, then \( \ln\left({H0}\right) = \ln\left({1}\right) = 0 \) and therefore the formula is: $$ z=\frac{ | \ln\left({RR}\right) - \ln\left({1}\right)| }{SE(\ln\left({RR}\right))} =\frac{ | \ln\left({RR}\right) - 0 | }{SE(\ln\left({RR}\right))} = \frac{ | \ln\left({RR}\right) | }{SE(\ln\left({RR}\right))} $$The p-value corresponding to the z-value is: $$ p=2 \cdot \int_z^{\infty} \frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2} \cdot x^2} dx $$Odds:The odds of disease (D) given that exposure (E) has occurred: $$ Odds_1 = \frac{P(D \: | \: E)}{1 - P(D \: | \: E)} = \frac{P(D \: | \: E)}{P(not \: D \: | \: E)} = \frac{\: \frac{d_1}{n_1} \:}{\frac{h_1}{n_1}} = \frac{d_1 \cdot n_1}{h_1 \cdot n_1} = \frac{d_1}{h_1} $$The odds of disease (D) given that exposure (E) has NOT occurred: $$ Odds_2 = \frac{P(D \: | not \: E)}{1 - P(D \: | not \: E)} = \frac{P(D \: | not \: E)}{P(not \: D \: | not \: E)} = \frac{\: \frac{d_2}{n_2} \:}{\frac{h_2}{n_2}} = \frac{d_2 \cdot n_2}{h_2 \cdot n_2} = \frac{d_2}{h_2} $$Standard error of logarithmic transformed odds: $$ SE(\ln(odds_1)) = \sqrt{\frac{1}{d_1}+\frac{1}{h_1}} \;\;\; \text{and} \;\;\; SE(\ln(odds_2))=\sqrt{\frac{1}{d_2}+\frac{1}{h_2}} $$95 % Confidence Interval of logarithmic transformed odds: $$ 95\; \% \;CI = \left[ \ln(odds) - 1.96 \cdot SE(\ln(odds)) \;\; : \;\; \ln(odds) + 1.96 \cdot SE(\ln(odds))\right] $$95 % Confidence Interval of odds: $$ 95 \; \% \; CI = \left[ \text{e}^{\ln(odds) - 1.96 \cdot SE(\ln(odds))} : \text{e}^{\ln(odds) + 1.96 \cdot SE(\ln(odds))}\right] $$or, alternatively: $$ 95\; \% \;CI = \left[\frac{odds}{\text{e}^{1.96 \cdot SE(\ln(odds))}} \;\; : \;\; odds \cdot \text{e}^{1.96 \cdot SE(\ln(odds))}\right] $$Odds Ratio$$ OR = \frac{Odds_1}{Odds_2} = \frac{\frac{d_1}{h_1}}{\frac{d_2}{h_2}}=\frac{d_1 \cdot h_2}{h_1 \cdot d_2} $$ Standard Error of the logarithmic transformed OR, ln(OR): $$ SE(\ln\left({OR}\right)) = \sqrt{\frac{1}{d_1}+\frac{1}{h_1}+\frac{1}{d_2}+\frac{1}{h_2}} $$95 % Confidence Interval of ln(OR): $$ 95 \; \% \; CI = \left[ \ln\left({OR}\right) - 1.96 \cdot SE(\ln\left({OR}\right)) : \ln\left({OR}\right) + 1.96 \cdot SE(\ln\left({OR}\right)) \right] $$95 % Confidence Interval of OR: $$ 95 \; \% \; CI = \left[ e^{\ln\left({OR} - 1.96 \cdot SE(\ln\left({OR}\right))\right)} : e^{\ln\left({OR}\right) + 1.96 \cdot SE(\ln\left({OR}\right))}\right] $$or, (alternatively): $$ 95 \; \% \; CI = \left[\frac{OR}{e^{1.96 \cdot SE(\ln\left({OR}\right))}} : OR \cdot e^{1.96 \cdot SE(\ln\left({OR}\right))}\right] $$Calculation of z-value in the general case, where the null hypothesis is H0: $$ z = \frac{| \ln\left({OR}\right) - \ln\left({H0}\right)|}{SE(\ln\left({OR}\right))} $$In the standard case where H0 = 1, then \( \ln\left({H0}\right) = \ln\left({1}\right) = 0 \) and therefore the formula is: $$ z=\frac{ | \ln\left({OR}\right) - \ln\left({1}\right)| }{SE(\ln\left({OR}\right))} =\frac{ | \ln\left({OR}\right) - 0 | }{SE(\ln\left({OR}\right))} = \frac{ | \ln\left({OR}\right) | }{SE(\ln\left({OR}\right))} $$The p-value corresponding to the z-value is: $$ p=2 \cdot \int_z^{\infty} \frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2} \cdot x^2} dx $$Test, if two OR could be equal: In other words; H0: OR1 = OR2 $$ z=\frac{\ln\left({OR_1} \right) - \ln\left({OR_2} \right)}{\sqrt{SE\left(\ln\left({OR_1}\right)\right)^2 + SE\left(\ln\left({OR_2}\right)\right)^2}} $$Or, alternatively: $$ z = \frac{\ln\left({\frac{OR_1}{OR_2}}\right)}{\sqrt{SE\left(\ln\left({OR_1}\right)\right)^2 + SE\left(\ln\left({OR_2}\right)\right)^2}} $$The corresponding p-value is: $$ p=2 \cdot \int_{z}^{\infty} \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2} \cdot x^2} dx $$95 % Confidence Interval of the difference "ln(OR1) - ln(OR2)": Standard Error of this difference: $$ SE\left(\text{Diff}_{\ln\left({OR}\right)}\right) = \sqrt{SE\left(\ln\left({OR_1}\right)\right)^2 + SE\left(\ln\left({OR_2}\right)\right)^2} $$95 % CI of Diffln(OR): (The number 0 will be in this interval if H0 is true) $$ 95 \; \% \; CI = \left[\text{Diff}_{\ln\left({OR}\right)} - 1.96 \cdot SE\left(\text{Diff}_{\ln\left({OR}\right)}\right) \; \; : \;\; \text{Diff}_{\ln\left({OR}\right)} + 1.96 \cdot SE\left(\text{Diff}_{\ln\left({OR}\right)}\right) \right] $$Exponentiated: (This will be the 95 % CI of the Ratio \( \frac{OR_1}{OR_2} \) ). The number 1 will be in this interval if H0 is true. $$ 95 \; \% \; CI = \left[ \text{e}^{\text{Diff}_{\ln\left({OR}\right)} - 1.96 \cdot SE\left(\text{Diff}_{\ln\left({OR}\right)}\right) } \;\; : \;\; \text{e}^{\text{Diff}_{\ln\left({OR}\right)} + 1.96 \cdot SE\left(\text{Diff}_{\ln\left({OR}\right)}\right) } \right] $$ $$ = \left[ \exp\left({\text{Diff}_{\ln\left({OR}\right)} - 1.96 \cdot SE\left(\text{Diff}_{\ln\left({OR}\right)}\right) }\right) \;\; : \;\; \exp\left({\text{Diff}_{\ln\left({OR}\right)} + 1.96 \cdot SE\left(\text{Diff}_{\ln\left({OR}\right)}\right) }\right) \right] $$Sensitivity & Specificity
Calculate sensitivity, specificity and all other concepts described below HERE.
Disease Prevalence (the proportion of the sample that has the disease): $$ DP = \frac{TP + FN}{N} $$Sensitivity. This is the probability that you test positive given the fact that you have the disease. It is the same as the power (1 - β) of the test: $$ Sensitivity = \frac{TP}{TP + FN} $$Specificity. The probability that you test negative given the fact that you don't have the disease: $$ Specificity = \frac{TN}{FP + TN} $$Positive Predictive Value. The probability that you have the disease given the fact that you tested positive.: $$ PPV = \frac{TP}{TP + FP} $$Negative Predictive Value. The probability that you don't have the disease given the fact that you tested negative: $$ NPV = \frac{TN}{FN + TN} $$Accuracy. The probability that the test gives the correct answer (be it either positive or negative): $$ Accuracy = \frac{TP + TN}{N} $$False Positive Rate. The probability that you test positive given the fact that you don't have the disease. This is the same as the risk of type 1 error (the significance level, α): $$ FPR = \frac{FP}{FP + TN} $$False Negative Rate. The "miss rate". The probability that you test negative given the fact that you have the disease. This is the same as the risk of type 2 error (β): $$ FNR = \frac{FN}{TP + FN} $$False Discovery Rate. The probability that you don't have the disease given the fact that you tested positive: $$ FDR = \frac{FP}{TP + FP} $$False Omission Rate. The probability that you have the disease given the fact that you tested negative: $$ FOR = \frac{FN}{FN + TN} $$All of the above concepts are risks/proportions and therefore they have corresponding standard errors. These can be found using the formulas under section "Standard error of proportion" under "Proportions" above. After having found the SE the 95 % Confidence Intervals can be calculated as described under "Proportions". Positive Likelihood Rate. The probability that a person with the disease tests positive divided by the probability that a person without the disease tests positive. If the rate is greater than 1 the test is more likely to give a true positive than a false positive. If the rate is between 0 and 1 the test is more likely to give a false positive than a true positive: $$ LR+ = \frac{TPR}{FPR} = \frac{sensitivity}{1 - specificity}$$Negative Likelihood Ratio. The probability that a person with the disease tests negative divided by the probability that a person without the disease tests negative. If the rate is greater than 1 the test is more likely to give a false negative than a true negative. If the rate is between 0 and 1 the test is more likely to give a true negative than a false negative: $$ LR- = \frac{FNR}{TNR} = \frac{1 - sensitivity}{specificity} $$Diagnostic Odds Ratio. The rate between the odds of a person testing positive who has the disease relative to the odds of a person testing positive who do not have the disease: $$ DOR = \frac{LR+}{LR-} $$F1 Score. This is used as a single measure of performance of the test for the positive class. It is a measure of the test's accuracy: $$ F_1 = 2 \cdot \frac{PPV \cdot sensitivity}{PPV + sensitivity} $$Power. The power of the test is the probability that you test positive given the fact that you have the disease. It's the same as the sensitivity. : $$ Power = 1 - \beta = sensitivity $$Means
Compare two or more already known mean values with a z-test and a t-test HERE.
Calculate mean, standard deviation and confidence intervals from input data sets and perform z-test and a t-test HERE. Mean value \( \bar{x} \) of sample or data set consisting of n numbers: $$ \bar{x} = \frac{x_1 + x_2 + x_3 + ... + x_n}{n} $$Variance of sample: (the variance is the average of the squared distances to the mean value). $$ Var(x)=\sum_{i=1}^n {\frac{\left( x_i - \bar{x} \right)^2}{n-1}} $$or (as an alternative): $$ Var(x)=\frac{\sum_{i=1}^n{\left(x_i^2\right)} - n \cdot \bar{x}^2}{n-1} $$This is slightly different from the variance of a population, which is: $$ Var(x)=\sum_{i=1}^n {\frac{\left( x_i - \bar{x} \right)^2}{n}} = \frac{\sum_{i=1}^n{\left(x_i^2\right)} - n \cdot \bar{x}^2}{n}$$Standard Deviation, SD, of a sample (SD is the average of the distances to the mean value): $$ SD = \sqrt{Var\left( x \right) } $$The number \( \sqrt{Var\left( x \right) } \) is (in this case) the variance of the sample, see above. The SD of a population is found with the same formula, but by using the variance of the population in the formula instead. 95 % Confidence Interval of a Standard Deviation: $$ 95 \; \% \; CI = \left[ SD \cdot \sqrt{\frac{DF}{(\chi^2)_1}} \; : \; SD \cdot \sqrt{\frac{DF}{(\chi^2)_2}} \right] $$where DF = n - 1 is the degree of freedom and the numbers \( \chi^2_1 \) and \( \chi^2_2 \) are the 97.5 and 2.5 percent quantiles of the cumulative chi-square probability distribution. In other words: $$ 0.975 = \int_{0}^{\chi^2_1} {\left( \frac{x^{\frac{1}{2} \cdot df - 1} \cdot \text{e}^{-\frac{1}{2} \cdot x}}{2^{\frac{1}{2} \cdot df} \cdot \Gamma\left(\frac{df}{2}\right)} \right) dx} \;\; \text{and} \;\; 0.025 = \int_{0}^{\chi^2_2} {\left( \frac{x^{\frac{1}{2} \cdot df - 1} \cdot \text{e}^{-\frac{1}{2} \cdot x}}{2^{\frac{1}{2} \cdot df} \cdot \Gamma\left(\frac{df}{2}\right)} \right) dx}$$For an explanation of the number Γ (Gamma) please see section "F Test". To test whether a given SD could be equal to a certain number SD0 we calculate the chi square value: $$ \chi^2 = \frac{SD^2}{SD_0^2} \cdot DF $$The corresponding p-value is two times the smallest of the numbers p1 and p2 $$ p_1 = \int_{\chi^2}^\infty {\left( \frac{x^{\frac{1}{2} \cdot df - 1} \cdot \text{e}^{-\frac{1}{2} \cdot x}}{2^{\frac{1}{2} \cdot df} \cdot \Gamma\left(\frac{df}{2}\right)} \right) dx} \;\; \text{and} \;\; p_2 = 1 - p_1 $$If the p-value is smaller than 0.05 we can reject the null hypothesis H0: SD = SD0. Standard error of a mean value from a sample: $$ SE=\frac{SD}{\sqrt{n}} $$95 % Confidence Interval of Mean: $$ 95 \; \% \; CI=\left[ \bar{x} - 1.96 \cdot SE : \bar{x} + 1.96 \cdot SE \right] $$The "mean difference" between two samples: $$ MD = Mean_1 - Mean_2$$This number will be negative if Mean1 < Mean2. In that case you could swap the order: \(MD = Mean_2 - Mean_1\). Standard Error of Mean Difference: $$ SE_{MD}=\sqrt{\left( SE_1 \right)^2 + \left(SE_2\right)^2 } $$95 % CI of Mean Difference:
Z-test:z-value, testing if two means are equal: $$ z=\frac{|MD|}{SE_{MD}}=\frac{|Mean_1 - Mean_2|}{\sqrt{\left(SE_1\right)^2 + \left(SE_2 \right)^2}} $$This is equivalent to testing the null hypothesis, that MD is equal to 0, i.e. H0: MD = 0 p-value corresponding to this z-value: $$ p = 2 \cdot \int_z^\infty {\frac{1}{\sqrt{2\pi}} \text{e}^{-\frac{1}{2}x^2} dx} $$If the null hypothesis is NOT H0: MD = 0 but instead H0: MD > 0 or H0: MD < 0 the z-value is found in the same way, only without the numerical signs: $$ z = \frac{MD - 0}{SE_{MD}} = \frac{Mean_1 - Mean_2 - 0}{\sqrt{\left(SE_1\right)^2 + \left(SE_2 \right)^2}} = \frac{Mean_1 - Mean_2}{\sqrt{\left(SE_1\right)^2 + \left(SE_2 \right)^2}}$$This z-value can then be either negative or positive. If H0 says that MD > 0 then the p-value is calculated as the integral: $$ p = \int_{-\infty}^{z} {\frac{1}{\sqrt{2\pi}} \text{e}^{-\frac{1}{2}x^2} dx} $$In other words the area under the normal distribution curve from minus infinity to z. If H0 says that MD < 0 then the p-value is calculated as the integral: $$ p = \int_z^\infty {\frac{1}{\sqrt{2\pi}} \text{e}^{-\frac{1}{2}x^2} dx} $$In other words the area under the curve from z to infinity. In the general case, if the null hypothesis says that MD = z0 for some number z0 the z-value is found as: $$ z = \frac{|MD - z_0|}{SE_{MD}} = \frac{|Mean_1 - Mean_2- z_0|}{\sqrt{\left(SE_1\right)^2 + \left(SE_2 \right)^2}} $$And the corresponding p-value is: $$ p = 2 \cdot \int_z^\infty {\frac{1}{\sqrt{2\pi}} \text{e}^{-\frac{1}{2}x^2} dx} $$If the null hypothesis says that MD > z0 the z-value is: $$ z = \frac{MD - z_0}{SE_{MD}} = \frac{Mean_1 - Mean_2- z_0}{\sqrt{\left(SE_1\right)^2 + \left(SE_2 \right)^2}} $$And the p-value will be: $$ p = \int_{-\infty}^{z} {\frac{1}{\sqrt{2\pi}} \text{e}^{-\frac{1}{2}x^2} dx} $$If the null hypothesis says that MD < z0 the z-value is: $$ z = \frac{MD - z_0}{SE_{MD}} = \frac{Mean_1 - Mean_2- z_0}{\sqrt{\left(SE_1\right)^2 + \left(SE_2 \right)^2}} $$And the p-value is found as: $$ p = \int_z^\infty {\frac{1}{\sqrt{2\pi}} \text{e}^{-\frac{1}{2}x^2} dx} $$F-test:Using an F-test to see if two variances \( Var_1 = {({SD}_1})^{2} \) and \( Var_2 = {({SD}_2})^{2} \) from two samples could be equal: First, the degrees of freedom of the two samples are found as \( df_1 = n_1 - 1 \) and \( df_2 = n_2 - 1 \), where \( n_1 \) and \( n_2 \) are the sample sizes. The first number \( f_1 \) in the f-test is calculated as: $$ f_1 = \frac{(SD_1)^2}{(SD_2)^2} $$The second number \( f_2 \) in the f-test is calculated as: $$ f_2 = \frac{(SD_2)^2}{(SD_1)^2} = \frac{1}{f_1} $$The p-value \( p_1 \) corresponding to \( f_1 \) is the smallest of the two following numbers: $$ p=\int_{f_1}^\infty{\left( \frac{df_1^{\frac{df_1}{2}} \cdot df_2 ^\frac{df_2}{2} \cdot \Gamma \left(\frac{df_1 + df_2}{2}\right) \cdot x^{\frac{df_1}{2}-1}}{\Gamma \left(\frac{df_1}{2}\right) \cdot \Gamma \left(\frac{df_2}{2}\right) \cdot \left(df_2 + df_1 \cdot x\right)^{\frac{df_1 + df_2}{2}}} \right) dx} \; \; \; \; \; \; \text{and} \;\;\;\;\;\; 1-p $$The Gamma number in the expression is in its general form \( \Gamma{\left( \frac{k}{2}\right)} \) calculated as follows: $$ \Gamma\left(\frac{k}{2}\right) = \begin{cases} \; \sqrt{\pi} & , \text{if $k = 1$} \\[2ex] \; 1 & , \text{if $ k = 2$} \\[2ex] \; (\frac{4}{2} - 1) \cdot (\frac{6}{2} - 1) \cdot (\frac{8}{2} - 1) \cdot \cdots \cdot (\frac{k}{2} - 1) & , \text{if $k$ is even and greater than 2} \\[2ex] \; \sqrt{\pi} \cdot (\frac{3}{2} - 1) \cdot (\frac{5}{2} - 1) \cdot (\frac{7}{2} - 1) \cdot \cdots \cdot (\frac{k}{2} - 1) & , \text{if $k$ is odd and greater than 1} \end{cases} $$The p-value \( p_2 \) corresponding to the f-value \( f_2 \) is the smallest of the two following numbers: $$ p = \int_{f_2}^\infty {\left( \frac{df_1^{\frac{df_1}{2}} \cdot df_2 ^\frac{df_2}{2} \cdot \Gamma \left(\frac{df_1 + df_2}{2}\right) \cdot x^{\frac{df_1}{2}-1}}{\Gamma \left(\frac{df_1}{2}\right) \cdot \Gamma \left(\frac{df_2}{2}\right) \cdot \left(df_2 + df_1 \cdot x\right)^{\frac{df_1 + df_2}{2}}} \right) dx} \;\;\;\;\;\; \text{and} \;\;\;\;\;\; 1-p $$The overall p-value of the F-test is: $$ p = p_1 + p_2 $$T-test:If the F-test shows that the two populations could have the same variance then the common variance, \( Var_c \) , is calculated: $$ {Var}_c=\frac{(df_1) \cdot (SD_1)^2 + (df_2) \cdot (SD_2)^2}{{df}_1 + {df}_2} = \frac{(n_1 - 1) \cdot (SD_1)^2 + (n_2 - 1) \cdot (SD_2)^2}{n_1 + n_2 - 2} $$If desired, one could also calculate the common SD as well: $$ {SD}_c = \sqrt{{Var_c}} = \sqrt{\frac{(df_1) \cdot (SD_1)^2 + (df_2) \cdot (SD_2)^2}{{df}_1 + {df}_2}} $$The Mean Difference is: $$ MD = {Mean}_1 - {Mean}_2 $$The Standard Error of the Mean Difference (in this case, assuming same variance in both samples) is calculated as one of the 4 expressions: $$ \begin{align} {SE}_{MD} & = \sqrt{\left(\frac{{(SD_c)}^2}{n_1} + \frac{{(SD_c)}^2}{n_2} \right)} \\ & = \sqrt{{(SD_c)}^2 \cdot \left(\frac{1}{n_1} + \frac{1}{n_2} \right)} \\ & = \sqrt{(SD_c)^2} \cdot \sqrt{\left( \frac{1}{n_1} + \frac{1}{n_2} \right)} \\ & = {SD}_c \cdot \sqrt{\left( \frac{1}{n_1} + \frac{1}{n_2} \right)} \end{align} $$The 95 % Confidence Interval of MD is: $$ 95 \; \% \; CI = \left[ MD - t_{(1-\frac{\alpha}{2})} \cdot {SE}_{MD} \; : \; MD + t_{(1-\frac{\alpha}{2})} \cdot {SE}_{MD} \right] $$The number \( t_{(1-\frac{\alpha}{2})} \) is the quantile in the t-distribution with \( n_1 + n_2 - 2 \) degrees of freedom corresponding to the significance level α . For example, if α = 0.05 then 1 - α/2; = 1 - 0.025 = 0.975, in other words the 97.5 % quantile The t-value in the t-test is calculated using this formula: $$ t = \frac{|MD|}{{SE}_{MD}} $$and finally the corresponding p-value is calculated as: $$ p = 2 \cdot \int_{t}^\infty { \left( \frac{\Gamma{\left( \frac{df+1}{2}\right)}}{\sqrt{\pi \cdot df} \cdot \Gamma{\left(\frac{df}{2}\right)} \cdot \left( 1 + \frac{x^2}{df}\right)^{(df+1)/2}} \right) dx} $$where \( df \) is the total degree of freedom for both samples: \( df = {df}_1 + {df}_2 = n_1 + n_2 - 2 \) . If (on the other hand) the F-test shows the two variances \( {({SD}_1})^{2} \) and \( {({SD}_2})^{2} \) can NOT be assumed equal, then the Standard Error of MD is found in the following way: $$ {SE}_{MD} = \sqrt{\frac{(SD_1)^2}{n_1} + \frac{(SD_2)^2}{n_2}} = \sqrt{(SE_1)^2 + (SE_2)^2} $$The degrees of freedom can, in this case, be found as a sort of weighted average between the two DF's of the groups: $$ DF = \frac{((SE_1)^2 + (SE_2)^2)^2}{ \frac{(SD_1)^4}{n_1 \cdot n_1 \cdot (n_1 - 1)} + \frac{(SD_2)^4}{n_2 \cdot n_2 \cdot (n_2 - 1)}} = \frac{((SE_1)^2 + (SE_2)^2)^2}{ \frac{(SE_1)^4}{n_1 - 1} + \frac{(SE_2)^4}{n_2 - 1}} $$And the 95 % CI of the Mean Difference will then be: $$ 95 \; \% \; CI = \left[ MD - t_{(1-\frac{\alpha}{2})} \cdot {SE}_{MD} \; : \; MD + t_{(1-\frac{\alpha}{2})} \cdot {SE}_{MD} \right] $$The t-value in this case (assuming different variances in the two samples) is found using the same formula as above (but with the modified version of SEMD): $$ t = \frac{|MD|}{{SE}_{MD}} $$and the corresponding p-value is: $$ p = 2 \cdot \int_{t}^\infty { \left( \frac{\Gamma{\left(\frac{df+1}{2}\right)}}{\sqrt{\pi \cdot df} \cdot \Gamma{\left(\frac{df}{2}\right)} \cdot \left( 1 + \frac{x^2}{df}\right)^{(df+1)/2}}\right) dx} $$The above procedure dealt with the case where the null hypothesis stated that MD = 0 If you want to test a different null hypothesis in the t-test, for example H0: MD > 0 or H0: MD < 0 then please look under "z-test" above for an overview of the procedures, since the procedures will be the same, only the formulas for t and p correspondingly adjusted. Confidence Intervals
Calculate confidence intervals for means, proportions and slopes HERE.
Confidence Interval of a MeanFor a given significance level alpha (α) the (100 - α) % approximated confidence interval of a mean value \( \bar{x} \) is: $$\left[ \bar{x} - z_{(1-\frac{\alpha}{2})} \cdot SE : \bar{x} + z_{(1-\frac{\alpha}{2})} \cdot SE \right] $$The number \( z_{(1 - \frac{\alpha}{2})}\) is the \(1 - \frac{\alpha}{2}\) quantile of the standard normal distribution N(0,1). Standard Error of a mean is \( SE = \frac{SD}{\sqrt{n}}\) where SD is the standard deviation and n is the sample size. For example: If \(\alpha = 5\%\) then \( z_{(1 - \frac{\alpha}{2})} = z_{(1 - \frac{0.05}{2})} = z_{0.975} = 1.96\) . Therefore, in this case, the 95 % approximated Confidence Interval of a mean will be: $$ 95 \; \% \; CI=\left[ \bar{x} - 1.96 \cdot SE : \bar{x} + 1.96 \cdot SE \right] $$If you want the exact confidence interval (using the t-distribution) instead of the approximated interval above, it is: $$\left[ \bar{x} - t_{(1-\frac{\alpha}{2})} \cdot SE : \bar{x} + t_{(1-\frac{\alpha}{2})} \cdot SE \right] $$Here, the number \( t_{(1 - \frac{\alpha}{2})}\) is the \(1 - \frac{\alpha}{2}\) quantile of the t-distribution with DF = N - 2 degrees of freedom. N is the sample size. For example: If \(\alpha = 5\%\) and DF = 14 then \( t_{(1 - \frac{\alpha}{2})} = t_{(1 - \frac{0.05}{2})} = t_{0.975} = 2.145\). This 97.5 % quantile can also be found via the section "Tables" in the menu. In this case, the 95 % exact Confidence Interval of a given mean will be: $$ 95 \; \% \; CI=\left[ \bar{x} - 2.145 \cdot SE : \bar{x} + 2.145 \cdot SE \right] $$Confidence Interval of a ProportionAfter having chosen the desired significance level α (often 5 %) the (100 - α) % approximated confidence interval of a proportion \( \hat{p} \) is: $$\left[ \hat{p} - z_{(1-\frac{\alpha}{2})} \cdot SE : \hat{p} + z_{(1-\frac{\alpha}{2})} \cdot SE \right] $$Standard Error of a proportion \( \hat{p} \) is \( SE = \frac{\sqrt{\hat{p}(1 - \hat{p})}}{n}\) where n is the sample size. For an explanation of the number \( z_{(1-\frac{\alpha}{2})} \) please see above under "Confidence Interval of a Mean" The (100 - α) % exact confidence interval of a proportion \( \hat{p} \) is: $$\left[ \hat{p} - t_{(1-\frac{\alpha}{2})} \cdot SE : \hat{p} + t_{(1-\frac{\alpha}{2})} \cdot SE \right] $$Using the t-distribution. For an explanation of the number \( t_{(1-\frac{\alpha}{2})} \) please see above under "Confidence Interval of a Mean" Confidence Interval of a Slope (β value)After a linear regression the regression line will on the form \( Y = \beta X + constant \: (+ error) \) . The number β is the slope (regression coefficient) and the constant is the intersection with the Y axis. For a significance level α the (100 - α) % approximated confidence interval of the slope β is: $$\left[ \beta - z_{(1-\frac{\alpha}{2})} \cdot SE \: : \: \beta + z_{(1-\frac{\alpha}{2})} \cdot SE \right] $$Standard Error of a slope β (regression coefficient) is: $$SE = |\beta| \cdot \sqrt{\frac{1 - R^2}{DF \cdot R^2}} , $$where DF = N - 2 is the degrees of freedom, N the number of points (x,y) and R2 is the correlation coefficient. For an explanation of the number \( z_{(1-\frac{\alpha}{2})} \) please see above under "Confidence Interval of a Mean" The (100 - α) % exact confidence interval of the slope β is: $$\left[ \beta - t_{(1-\frac{\alpha}{2})} \cdot SE \: : \: \beta + t_{(1-\frac{\alpha}{2})} \cdot SE \right] $$Using the t-distribution. For an explanation of the number \( t_{(1-\frac{\alpha}{2})} \) please see above under "Confidence Interval of a Mean" Chi-Square-Test
Perform chi-squared test of independence between two variables HERE.
Perform goodness-of-fit test to see whether an observed data set follows a known distribution HERE.
After having found the expected values, the number \(\chi^2 \) (chi square) is calculated as follows: $$ \chi^2=\sum_{h=1}^i{\left(\sum_{k=1}^j {\frac{\left(O_{hk}-E_{hk}\right)^2}{E_{hk}}} \right)} $$In other words: the sum of the squared distances between the observed values and the expected values relative to the expected values. Like this: $$ \chi^2 = \frac{\left(O_{11}-E_{11}\right)^2}{E_{11}} + \frac{\left(O_{12}-E_{12}\right)^2}{E_{12}} + ... + \frac{\left(O_{1j}-E_{1j}\right)^2}{E_{1j}} + ... $$ $$ ... + \frac{\left(O_{21}-E_{21}\right)^2}{E_{21}} + \frac{\left(O_{22}-E_{22}\right)^2}{E_{22}} + ... + \frac{\left(O_{2j}-E_{2j}\right)^2}{E_{2j}} + ... $$ $$ ... + \frac{\left(O_{i1}-E_{i1}\right)^2}{E_{i1}} + \frac{\left(O_{i2}-E_{i2}\right)^2}{E_{i2}} + ... + \frac{\left(O_{ij}-E_{ij}\right)^2}{E_{ij}} $$The p-value corresponding to the chi-square-number is then found as follows: $$ p=\int_{\chi^2}^\infty {\left( \frac{x^{\frac{1}{2} \cdot df - 1} \cdot \text{e}^{-\frac{1}{2} \cdot x}}{2^{\frac{1}{2} \cdot df} \cdot \Gamma\left( \frac{df}{2}\right)} \right) dx} $$Weighted Average
Calculate the weighted average (weighted estimate) of two or more means, slopes, risk ratios, odds ratios ... etc. HERE.
The weighted estimate (or weighted average) of two estimates can be calculated as: $$ WE=\frac{estimate_1 \cdot w_1+estimate_2 \cdot w_2}{w_1 + w_2} $$where the weights w1 and w2 are calculated as $$ w_1=\frac{1}{(SE_1)^2} \; \text{ and } \; w_2=\frac{1}{(SE_2)^2} $$If the WE is of more than two estimates, then the general formula is used: $$ WE=\frac{\sum_{i=1}^n{\left(estimate_i \cdot w_i\right)}}{\sum_{i=1}^n{\left(w_i\right)}}= \frac{estimate_1 \cdot w_1+estimate_2 \cdot w_2+...+ estimate_n \cdot w_n}{w_1+w_2+... + w_n} $$The Standard Error of WE: $$ SE(WE) = \sqrt{\frac{1}{w_1+w_2+... + w_n}} $$The above formulas are used, if the estimates are of the type Mean Values, Mean Differences, Risk Differences, ... etc. where the weights are (in this particular case): $$ w_i=\frac{1}{SE(\ln\left({ estimate_i}\right))^2} $$After having found the number \( \ln\left({ WE }\right) \) one can find the real value of WE by exponentiating: $$ WE=\text{e}^{\ln\left({WE}\right)}=\exp\left({\ln\left({WE}\right) }\right) $$Standard Error of ln(WE): $$ SE\left( \ln\left({WE}\right) \right) = \sqrt{ \frac{1}{w_1 + w_2 + ... + w_n} } $$95 % CI of ln(WE): 95 % CI of WE : Test to see if the WE could be 1 or (consequently); ln(WE) = 0 (Meaning WE not significant) $$ z=\frac{\ln\left({WE}\right) - \ln\left({1}\right)}{SE\left(\ln\left({WE}\right)\right)} = \frac{\ln\left({WE}\right)}{SE\left(\ln\left({WE}\right)\right)} $$The corresponding p-value is: $$ p=2 \cdot \int_{z}^{\infty} \frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2} \cdot x^2} dx $$Data Analysis
Perform data analysis on one or more data sets HERE and calculate means, standard deviations, confidence intervals and do z-test, t-test and ANOVA.
QuartilesThe quartiles are the three numbers that divide a data set into four parts:
The best way to illustrate quartiles is probably with an example: If we have, say, 10 people and count the cups of coffee they had during a day, we get a table like this:
We see immediately that the number 4 is the mode of the data set, since it is the number of cups that occurs most times, namely 3.
Note that the persons' index numbers are no longer in ascending order. This, however, is not important for calculating the quartiles, since the quartiles are regarding the data values and not the index values. First we find the median: Since 10 is an even number, we divide the list into two parts with 5 in each
And because 10 is an even number, the median of the data set will in this case be the number in between 3 and 4, in other words the average of the two numbers, which is 3.5. This means that 50% of the people had 3.5 cups of coffee that day or less. Although, technically speaking, any number between 3 and 4 (including 3!) would qualify as a median for this data set, since 50% would still have had that many cups or less that day. To calculate the 25% quartile, Q1: We take the first 5 data values. Since 5 is an uneven/odd number, there is in this case a "natural" data value that divides the five numbers into two equal parts with two numbers in each. This natural divider is in this case the third value, namely 2: 25% (a quarter) had 2 cups or less that day.
The calculation of the 75% qurtile, Q3, runs similar: We take the last five data values. The "natural" divider of these five numbers is the 8th value, namely 4, since it divides into two equal parts with two numbers in each. The 75% quartile is therefore 4: 75 percent (three quarters) had 4 cups or less that day. The remaining 25% of the people had more than 4 cups that day.
We can finish by writing down the set of quartiles: (Q1, Q2, Q3) = (2, 3.5, 4) Apart from the set of quartiles one can also find any quantile of a data set. For example the 20% quantile: 20% of 10 is 2 people, in other words, the 20% quantile would in this case be 1, since 20% of the ten people had 1 cup of coffee or less. SkewnessSkewness of a data sample: $$ skewness = \frac{\sqrt{n(n-1)}}{n-2} \cdot \frac{\frac{1}{n} \sum_{i=1}^{n}(x_i - \bar{x})^3 }{\left( \frac{1}{n-1} \sum_{i=1}^{n}(x_i - \bar{x})^2 \right)^{3/2}} $$Since \( Var = SD^2 = \frac{1}{n-1} \sum_{i=1}^{n}(x_i - \bar{x})^2 \) is the variance of a sample this can also be written as: $$ skewness = \frac{\sqrt{n(n-1)}}{n-2} \cdot \frac{\frac{1}{n} \sum_{i=1}^{n}(x_i - \bar{x})^3 }{\left( SD^2 \right)^{3/2}} = \frac{\sqrt{n(n-1)}}{n-2} \cdot \frac{\frac{1}{n} \sum_{i=1}^{n}(x_i - \bar{x})^3 }{ SD^3 } $$A normal distribution has a skewness with the value 0. In other words; if a data set or sample is to be assumed normally distributed, it must have a skewness of 0 (or close to 0). KurtosisKurtosis of a data sample: $$ K = \frac{\frac{1}{n} \sum_{i=1}^{n}(x_i - \bar{x})^4 }{\left( \frac{1}{n} \sum_{i=1}^{n}(x_i - \bar{x})^2 \right)^{2}} $$Since \( Var_{pop} = SD_{pop}^2 = \frac{1}{n} \sum_{i=1}^{n}(x_i - \bar{x})^2 \) is the variance of a population this can also be written as: $$ K = \frac{\frac{1}{n} \sum_{i=1}^{n}(x_i - \bar{x})^4 }{\left( Var_{pop} \right)^{2}} = \frac{\frac{1}{n} \sum_{i=1}^{n}(x_i - \bar{x})^4 }{ SD_{pop}^4 } $$A normal distribution has a kurtosis with the value 3. In other words; if a data set or sample is to be assumed normally distributed, it must have a kurtosis of 3 (or close to 3). ANOVA (one-way)In a one-sided ANOVA (Analysis of Variance) it is invesitigated whether each observation in each of the groups (data sets) differ from the mean value of the group more than each group mean value differ from the overall mean of all the observations from all groups combined. This is done by using the F-distribution with the following number used as the F-statistics: $$ F = \frac{MSG}{MSW} $$With degrees of freedom DF1 = J - 1 and DF2 = n - J. J is the number of groups/data sets and n is the number of all observations in total for all groups combined. The number MSG (between-groups mean square) in the numerator is the average of the squared differences between each group mean and the overall mean: $$ MSG = \frac{SSG}{J - 1} = \frac{ \sum_{j=1}^J {n_j( \bar{x}_j - \bar{x} )^2} }{J - 1} $$Here, \( \bar{x}_j \) is the mean of the j'th group. \( \bar{x} \) is the overall mean of all the observations. Each squared difference \( (\bar{x}_j - \bar{x})^2 \) is weighted by multiplying by nj, the number of elements in the j'th group. The number SSG in the numerator is called the sum of squares between-groups. The number MSW (within-groups mean square) in the denominator is the mean of the sums of squared deviations from the mean values in all the J groups: $$ MSW = \frac{SSW}{n - J} = \frac{ \sum_{j=1}^J {\sum_{i=1}^{n_j} {(x_{ij} - \bar{x}_j )^2} } }{n - J} $$Here, \( x_{ij} \) is the i'th observation in the j'th group. \( \bar{x}_j \) is the mean of the j'th group. The number SSW in the numerator is called the sum of squares within-groups. The total sum of squares SST is the sum of squared differences between each of the total observations and the overall mean: $$ SST = \sum_{j=1}^J {\sum_{i=1}^{n_j} {(x_{ij} - \bar{x} )^2} } = SSG + SSW $$The P-value in the ANOVA one-way will then be calculated with the f-probability-density function: $$ p = \int_{F}^\infty {\left( \frac{df_1^{\frac{df_1}{2}} \cdot df_2 ^\frac{df_2}{2} \cdot \Gamma \left(\frac{df_1 + df_2}{2}\right) \cdot x^{\frac{df_1}{2}-1}}{\Gamma \left(\frac{df_1}{2}\right) \cdot \Gamma \left(\frac{df_2}{2}\right) \cdot \left(df_2 + df_1 \cdot x\right)^{\frac{df_1 + df_2}{2}}} \right) dx} $$ANOVA (two-way)In the two-way ANOVA two different F-values are calculated, F1 and F2: The F-value F1 is calculated as follows: $$ F_1 = \frac{MSG}{MSE} $$The numerator MSG is the mean value of the between-groups sum of squares: $$ MSG = \frac{SSG}{J - 1} = \frac{ I \cdot \sum_{j=1}^J {( \bar{x}_j - \bar{x} )^2} }{J - 1} $$In other words the average of the squared differences between each group mean \( \bar{x}_j \) and the overall mean \( \bar{x} \). The number I is the number of rows or "blocks" in the I × J matrix consisting of the J groups (data sets), each of size I. Note that in the two-way ANOVA all columns (data sets) must have the same size. The denominator MSE is the mean value of the error sum of squares: $$ MSE = \frac{SSE}{(J - 1)(I - 1)} = \frac{ \sum_{i=1}^I \sum_{j=1}^J {( x_{ij} - \bar{x}_j - (\bar{x}_i - \bar{x}) )^2} }{(J - 1)(I - 1)} $$Where \( \bar{x}_j \) is the mean of the j'th group and \( \bar{x}_i \) is the mean of the i'th row. The F-value F2, on the other hand, is calculated as follows: $$ F_2 = \frac{MSB}{MSE} $$The denominator MSE is the same as with F1. The numerator MSB is the mean value of the between-rows sum of squares: $$ MSB = \frac{SSB}{I - 1} = \frac{ J \cdot \sum_{i=1}^I {( \bar{x}_i - \bar{x} )^2} }{I - 1} $$In other words the average of the squared differences between each row (block) mean \( \bar{x}_i \) and the overall mean \( \bar{x} \). Furthermore, the number SST can be defined, which is the total sum of squares: SST = SSG + SSB + SSE P-values P1 and P2 can be calculated for both F1 and F2 respectively. If P1 is below the chosen significance level, the null hypotheis saying that there is no significant difference between the J group means can be rejected. If P2 is below the chosen significance level, the null hypotheis saying that there is no significant difference between the I row means can be rejected. Rates
Calculate the rates and confidence intervals of one or more groups HERE and test equality between rates.
Compare two incidence rates HERE by calculating their incidence rate ratio with confidence interval and test for equality.
Incidence Rate:$$ IR_1=\frac{c_1}{t_1} \;\;\; \text{and} \;\;\; IR_2=\frac{c_2}{t_2} $$ The standard error of the logarithmic transformed IR: $$ SE\left({\ln(IR_1)}\right) = \sqrt{\frac{1}{c_1}} = \frac{\sqrt{1}}{\sqrt{c_1}} = \frac{1}{\sqrt{c_1}} \;\;\;\;\; \text{and} \;\;\;\;\; SE\left({\ln(IR_2)}\right) = \sqrt{\frac{1}{c_2}} = \frac{\sqrt{1}}{\sqrt{c_2}} = \frac{1}{\sqrt{c_2}} $$95 % Confidence Interval of a logarithmic transformed Incidence Rate: $$ 95\; \% \;CI=\left[ \ln\left({IR}\right) - 1.96 \cdot SE\left({\ln(IR)}\right) \;\; : \;\; \ln\left({IR}\right) +1.96 \cdot SE\left({\ln(IR)}\right)\right] $$95 % Confidence Interval of the Incidence Rate: $$ 95\; \% \;CI=\left[\text{e}^{\ln\left({IR}\right) - 1.96 \cdot SE\left({\ln(IR)}\right)} \;\; : \;\; \text{e}^{\ln\left({IR}\right) + 1.96 \cdot SE\left({\ln(IR)}\right)} \right] $$or, consequently: $$ 95\; \% \;CI=\left[\frac{IR}{\text{e}^{1.96 \cdot SE\left({\ln(IR)}\right)}} \;\; : \;\; IR \cdot \text{e}^{1.96 \cdot SE\left({\ln(IR)}\right)} \right] $$Incidence Rate Ratio:$$ IRR=\frac{IR_1}{IR_2} $$ The Standard Error of the logarithmic transformed IRR: $$ SE\left({\ln(IRR)}\right) = \sqrt{\frac{1}{c_1} + \frac{1}{c_2} } $$95 % CI of the logarithmic transformed IRR: $$ 95\; \% \;CI=\left[ \ln\left({IRR}\right) - 1.96 \cdot SE\left({\ln(IRR)}\right) \;\; : \;\; \ln\left({IRR}\right) + 1.96 \cdot SE\left({\ln(IRR)}\right) \right] $$95 % CI of IRR: $$ 95\; \% \;CI=\left[\text{e}^{\ln\left({IRR}\right) - 1.96 \cdot SE\left({\ln(IRR)}\right)} \;\; : \;\; \text{e}^{\ln\left({IRR}\right) + 1.96 \cdot SE\left({\ln(IRR)}\right)} \right] $$or, consequently: $$ 95\; \% \;CI = \left[ \frac{IRR}{\text{e}^{1.96 \cdot SE\left({\ln(IRR)}\right)}} \;\; : \;\; IRR \cdot \text{e}^{1.96 \cdot SE\left({\ln(IRR)}\right)}\right] $$Z-Value, testing if the IRR could be equal to the null hypothesis H0: $$ z = \frac{| \; \ln\left({IRR}\right) - \ln\left({H0}\right) \; |}{SE\left({\ln(IRR)}\right)} $$The p-value corresponding to the z-value: $$ p = 2 \cdot \int_z^{\infty} \frac{1}{\sqrt{2\pi}} \cdot \text{e}^{-\frac{1}{2} \cdot x^2} dx $$Incidence Rate Difference:$$ IRD = IR_1 - IR_2 $$ Standard Error of the Incidence Rate Difference: $$ SE(IRD) = \sqrt{ \frac{c_1}{(t_1)^2} + \frac{c_2}{(t_2)^2} } $$or, consequently: $$ SE(IRD) = \sqrt{ \frac{IR_1}{t_1} + \frac{IR_2}{t_2} } $$95 % Confidence Interval of IRD: $$ 95\; \% \;CI=\left[ IRD - 1.96 \cdot SE(IRD) \;\; : \;\; IRD + 1.96 \cdot SE(IRD) \right] $$z-value, testing if IRD could be equal to the null hypothesis H0: $$ z = \frac{|IRD - H0|}{SE(IRD)} $$The corresponding p-value is: $$ p=2 \cdot \int_z^{\infty}\frac{1}{\sqrt{2\pi}} \cdot \text{e}^{-\frac{1}{2} \cdot x^2} dx $$Chi-Square-Test (in the case of Incidence Rates):First, the expected values are found:
Then the chi-square-number is calculated: $$ \chi^2 = \frac{(c_1 - e_1)^2}{e_1} + \frac{(c_2 - e_2)^2}{e_2} $$And then the p-value is found as the number: $$ p= \int_{\chi^2}^\infty {\left( \frac{x^{\frac{1}{2} \cdot df - 1} \cdot \text{e}^{-\frac{1}{2} \cdot x}}{2^{\frac{1}{2} \cdot df} \cdot \Gamma\left(\frac{df}{2}\right)} \right) dx} $$Mantel-Haenszel Stratified OR
Calculate Mantel-Haenszel odds ratio HERE from two or more strata and test the null hypothesis of OR = 1.
Mantel-Haenszel is a form of stratification to adjust for confounding via 2 × 2 tables that can be used if the sample sizes are very small, in other words if one or more of the cells in the 2 × 2 is below 5. After having perfomed the stratification, where we stratify after the possible confounder, we end up with n different 2 × 2 tables. Each of them has the following form:
Often there are only two tables, one containing all persons with the possible confounder and the other one containing all persons without the possible confounder. If, for example, "smoking status" is a possible confounder for a connection between an exposure and an outcome, we would have one table with all the smokers and the other table with all the non-smokers. Each table, corresponding to a specific stratum number, has its own OR value. If the OR values from all these tables differ from each other (are significantly different from each other) then the variable, that we stratified after (eg. "smoking status"), is an effect modifier. Because the effect that the exposure has on outcome will then be modified depending on with stratum you belong to. If this is the case, then the analysis will be completed with this conclusion, since a variable cannot be both an effect modifier AND a confounder. If, however, the OR values from the strata do not differ significantly from each other, then we can proceed to combine them by calculating their Mantel-Haenszel Weighted Estimate (weighted average). If this weighted estimate (ORWE) is significantly different from the crude OR (the OR value from the "original" 2 × 2 table without stratification) then the variable, that we stratified after, is a confounder The formula for the Mantel-Haenszel Weigthed OR: $$ OR_{WE} = \frac{\sum_{i=1}^n \left( w_i \cdot OR_i \right) }{\sum_{i=1}^n {w_i}} = \frac{\sum_{i=1}^n {\frac{d_{1i} \cdot h_{2i}}{n_i}} }{\sum_{i=1}^n {\frac{d_{2i} \cdot h_{1i}}{n_i}}} $$To find the 95 % Confidence Interval of the Mantel-Haenszel Weigthed OR we must find the standard error of the logarithmic transformed ORWE $$ SE(\ln(OR_{WE})) = \sqrt{\frac{V}{Q \cdot R}} \; \; , $$where $$ Q = \sum_{i=1}^n {\frac{d_{1i} \cdot h_{2i}}{n_i}} , R = \sum_{i=1}^n {\frac{d_{2i} \cdot h_{1i}}{n_i}} \: \text{ and } \: V = \sum_{i=1}^n {V_i} = \sum_{i=1}^n {\frac{d_{i} \cdot h_{i} \cdot n_{1i} \cdot n_{2i}}{n_{i}^2 \cdot (n_i - 1)}}$$Now the 95 % Confidence Interval of the logarithmic transformed ORWE will be: $$ 95 \% CI = [\ln(OR_{WE}) - 1.96 \cdot SE(\ln(OR_{WE})) \;\; : \;\; \ln(OR_{WE}) + 1.96 \cdot SE(\ln(OR_{WE}))] $$And the actual 95 % Confidence Interval will be the exponentialized version of this: $$ 95 \% CI = [\text{e}^{\ln(OR_{WE}) - 1.96 \cdot SE(\ln(OR_{WE}))} \;\; : \;\; \text{e}^{\ln(OR_{WE}) + 1.96 \cdot SE(\ln(OR_{WE}))}] $$or $$ 95 \% CI = \left[ \frac{OR_{WE}}{\text{e}^{1.96 \cdot SE(\ln(OR_{WE}))}} \;\; : \;\; OR_{WE} \cdot \text{e}^{1.96 \cdot SE(\ln(OR_{WE}))} \right] $$To test for homogeneity, i.e. to see if the OR values from the strata could be equal to each other, we perform a chi-square test of idenpendence where the number chi-square (χ2) is calculated as follows: $$ \chi^2 = \sum_{i=1}^n {\left( \frac{\ln(OR_i) - \ln(OR_{WE})}{SE(\ln(OR_i))} \right)^2 } $$The corresponding p-value is then found as the area under the χ2 propapility density function with DF = 1 degree of freedom from χ2 to infinity. Please see in the section "Chi-Square-Test" above. To test whether the calculated Weighted Estimate ORWE could be equal to 1, in other words to test whether the association between the exposure and the outcome is significant after having adjusted for the confounder, we perfom a chi-square test. The number χ2 in the test is calculated as follows: $$ \chi^2 = \frac{\left( \sum_{i=1}^n {(d_{1i})} - \sum_{i=1}^n {(E_{1i})} \right)^2}{\sum_{i=1}^n {(V_{i})}} = \frac{\left( \sum_{i=1}^n {(d_{1i})} - \sum_{i=1}^n {(E_{1i})} \right)^2}{\sum_{i=1}^n { \frac{d_{i} \cdot h_{i} \cdot n_{1i} \cdot n_{2i}}{n_{i}^2 \cdot (n_i - 1)} }} $$The corresponding p-value is then found as the area under the curve of the χ2 propapility density function with DF = 1 degree of freedom from χ2 to infinity. Please see in the section "Chi-Square-Test" above. The number Ei belonging to each of the i strata is the "expected value" that would have been instead of d1i if the proportion of outcome had been the same in both the exposed as in the unexposed group: $$ E_{1i} = \frac{d_i \cdot n_{1i} }{n_i} $$"Rule of Five"The "Rule of Five" is about the validity of the χ2 test performed on the ORWE. The validity of the test can be assessed by (for each stratum) calculating the following numbers: 1. min(di, n1i) (the minimum of the two numbers di and n1i) 2. max(0, n1i - hi) (the maximum of the two numbers 0 and n1i - hi). This will be 0 if n1i - hi is negative. The sum of all the minima is found, the sum of alle the maxima is found and the sum of all the expecyed values E is found: $$ \text{Sum}_{\text{min}} = \sum_{i=1}^n {(\text{min}_{i})} \;\; \text{ and } \;\; \text{Sum}_{\text{max}} = \sum_{i=1}^n {(\text{max}_{i})} \;\; \text{ and } \;\; \text{Sum}_{\text{E}} = \sum_{i=1}^n {(\text{E}_{1i})}$$The rule is that the absolute distance from both \( \text{Sum}_{\text{min}}\) and \( \text{Sum}_{\text{max}} \) to \( \text{Sum}_{\text{E}} \) must be 5 or more for the test to be valid: $$ \left|\text{Sum}_{\text{min}} - \text{Sum}_{\text{E}}\right| \geq 5 \;\; \text{ and } \;\; \left|\text{Sum}_{\text{max}} - \text{Sum}_{\text{E}}\right| \geq 5 $$Mann-Whitney (Wilcoxon) U Test
Perform Mann-Whitney U Test HERE. Both for small (N < 20) and large (N > 20) sample sizes.
Case: N < 20Mann-Whitney U Test is a method to test whether two data sets could be assumed equally distributed by comparing their ranks, if those data sets are not or cannot be assumed normally distributed. It is a non-parametric test, since parameters like for eg. the mean values do not figure as parameters, like in a z-test or t-test. If there are less than 20 numbers in each of the two sets, the following approach is used: For each single value in set 1 the number of values in set 2 that it is larger than is counted. A tie between two equal numbers is counted as 0.5. This number is U1. The very same procedure is used to calculate U2 by comparing each value in set 2 with each value in set 1. The smallest of U1 and U2 is then Uobt. (U obtained). By comparing this Uobt. with the critical value Ucrit. found in the table over critical U values below we can either reject or not reject the null hypothesis on a 5% or a 1% significance level. If Uobt. is smaller than or equal to Ucrit. the null hypothesis is rejected. The null hypothesis being: H0: The distribution of the two data sets are identical. The ranks are found by sorting the complete list consisting of all values from both n1 and n2 in ascending order. The lowest value (on position 1) will get rank 1, the next lowest rank 2, ... etc. In case there are ties (equal values) each of the equal values will be given the rank corresponding to the average of the positions of the tied values. In the table n1 is the size of data set 1 and n2 is the size of data set 2:
Case: N > 20In the case of larger sample sizes, N > 20, the principle is the same for calculating Uobt.: For each value in sample 1, count how many values in sample 2 are smaller than this. A tie counts as 0.5. This is then U1. For sample 2 the number U2 is found in a similar way. Uobt. is the smallest of U1 and U2. In the case of N > 20 there is, however, also a different way of finding the numbers U1 and U2: In the case of N > 20 there is, however, also an alternative to finding the numbers U1 and U2, namely in the shape of the formulas: $$ U_1 = R_1 - \frac{n_1(n_1 + 1)}{2} \text{ and } U_2 = R_2 - \frac{n_2(n_2 + 1)}{2} \; , $$where R1 and R2 are the sum of the ranks in sample 1 and sample 2. n1 and n2 are the sample sizes of sample 1 and sample 2. After having found Uobt. one can calculate its mean value mU and its standard deviation σU: $$ m_U = \frac{n_1 n_2}{2} \text{ and } \sigma_U = \sqrt{\frac{n_1 n_2 (n_1 + n_2 + 1)}{12}} $$If there are tied (equal) ranks in the list, the formula for σU will be instead: $$ \sigma_U = \sqrt{\frac{n_1 n_2}{12} \left( (n_1 + n_2 + 1) - \sum_{i=1}^{k}{ \frac{t_i^3 - t_i}{(n_1 + n_2)(n_1 + n_2 - 1)} } \right) } $$k is the number of distinct ranks that is shared by two or more values. ti is the number of values sharing rank number i. The P value is then found through a normal distribution approximation with the z-value found in this way: $$ z_U = \frac{| U_{obt.} - n_1 n_2 / 2 |}{\sqrt{n_1 n_2(n_1 + n_2 + 1)/12}} = \frac{| U_{obt.} - m_U |}{\sigma_U}$$The number f is the common language effect size. It is calculated this way: $$ f = \frac{U_1}{n_1 n_2} $$It expresses the percentage out of all possible ordered pairs (s1,s2) consisting of numbers s1 from sample 1 and s2 from sample 2 where s1 is larger than s2. The number r is the rank-biserial correlation. It is calculated this way: $$ r = f - u = 2f - 1 = \frac{2 U_1}{n_1 n_2} - 1 = 1 - \frac{2 U_2}{n_1 n_2} $$It is the difference between the effect size and its complement. Regression
Do linear and logistic regression HERE. Both singular as well as multiple regression.
Singular Linear RegressionIn the case where the dependent variable Y depends on only one independent variable X the model is: $$ Y = \beta_0 + \beta_1 X + \epsilon $$, where \( \beta_0 \) is the constant or the graphical intersection (intercept) with the Y-axis when the linear graph is
drawn and \( \beta_1 \) is the slope of the line. More precisely; \( \beta_0 \) is the Y-value in the point where the line intersects the Y-axis. The
point has the form \( (x, y) = (0, \beta_0) \). The number \( \epsilon \) is the error term, meaning the vertical distance from the predicted y value on
the line (that the model has given) to the actual y value (the y coordinate of the point).
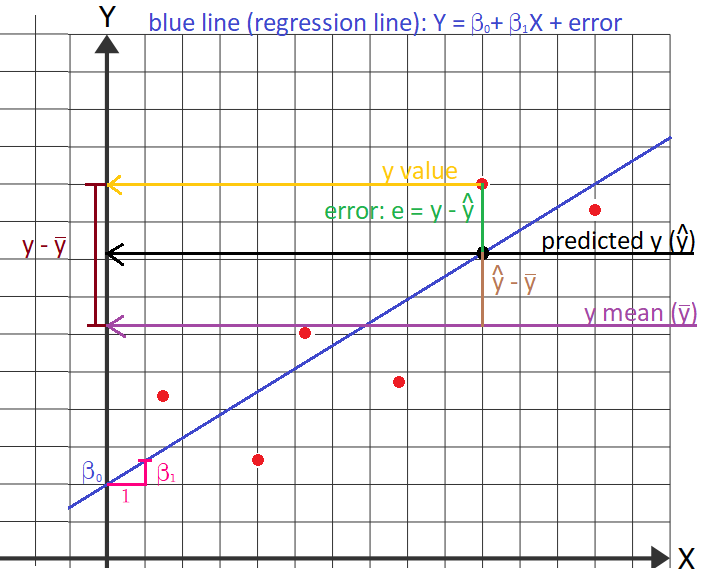
The formulas: $$ \beta_1 = \frac{\sum_{i=1}^n{(x_i - \bar{x})(y_i - \bar{y})}}{\sum_{i=1}^n{(x_i - \bar{x})^2}} $$ $$ \beta_0 = \bar{y} - \beta_1 \bar{x} $$ Meaning: In the numerator of the fraction of \( \beta_1 \), for each point (x, y) the distance from the x value to the
mean value of the x values is calculated and the distance from the y value to the mean of the y values is calculated. These distances are then multiplied
together and all these multiplied distances are added up.
To test the null hypothesis (H0) whether \( \beta_0 \) or \( \beta_1 \) could be equal to zero (or any other value), the following formula is used to find the t-values: $$ t = \frac{\beta_0 - H_0}{s(\beta_0)} $$where $$ s(\beta_0) = \sqrt{Var(\beta_0)} $$ $$ = \sqrt{\frac{1}{n-2}\left(\sum_{i=1}^n{(y_i - \bar{y})^2} - \frac{\left(\sum_{i=1}^n{(x_i - \bar{x})(y_i - \bar{y})}\right)^2}{\sum_{i=1}^n{(x_i - \bar{x})^2}}\right)} \sqrt{\frac{1}{n} + \frac{\bar{x}^2}{\sum_{i=1}^n{(x_i - \bar{x})^2}}} $$and $$ t = \frac{\beta_1 - H_0}{s(\beta_1)} $$where $$ s(\beta_1) = \sqrt{Var(\beta_1)} = \sqrt{ \frac{ \frac{1}{n-2}\left(\sum_{i=1}^n{(y_i - \bar{y})^2} - \frac{\left(\sum_{i=1}^n{(x_i - \bar{x})(y_i - \bar{y})}\right)^2}{\sum_{i=1}^n{(x_i - \bar{x})^2}}\right) }{ \sum_{i=1}^n{(x_i - \bar{x})^2} } } $$It can be shown that in the case of \( \beta_1 \) the formula for \( s(\beta_1) \) is equivalent to: $$ s(\beta_1) = |\beta_1| \cdot \sqrt{ \frac{1}{n-2} \cdot \frac{1 - R^2}{R^2}} $$In both of these cases, after having found the t-values, the t-test can then be performed with \( n - 2 \) degrees of freedom to find the corresponding p-value (se section "t-test" in chapter "means"). The correlation coefficient R2 of the linear regression is found this way: $$ R^2 = 1 - \frac{\sum_{i=1}^n{e_i^2}}{\sum_{i=1}^n{(y_i - \bar{y})^2}} = 1 - \frac{\sum_{i=1}^n{(y_i - \widehat{y_i})^2}}{\sum_{i=1}^n{(y_i - \bar{y})^2}} $$The numerator of the fraction is the sum of the squared errors. These errors are the vertical distances from each y value
to the predicted y value \( \hat{y} \) (the y value on the line, i.e. the y value that the point should have had if it had been on the line). The
denominator is the sum of the squared vertical distances between each y and the y mean.
And vice versa: The closer R2 is to zero the further away the points will be from the regression line. For at given x we can calculate the predicted y-value from the model: $$ \hat{y} = \beta_0 + \beta_1 \cdot x $$This is the value that y should have, if it were to lie exactly on the regression line. This predicted y-value has a confidence interval: $$ CI = \hat{y} \; \pm \; t_{(1-\frac{\alpha}{2})} \cdot SE_{\hat{y}} $$The number \( t_{(1-\frac{\alpha}{2})} \) is the \( (1-\frac{\alpha}{2})\cdot 100 \% \) quantile of the t-distribution with (n - 2) degrees of freedom and significance level α. See section "t-test" in chapter "means" above for further info. \( SE_{\hat{y}} \) is the standard error of the predicted y. It has the formula: $$ SE_{\hat{y}} = \sqrt{ s^2 \left( 1 + \frac{1}{n} + \frac{ (x - \bar{x})^2 }{\sum_{i=1}^n{x_i^2} - n\bar{x}^2} \right)} $$Where x is the x-value from the point \( (x, \hat{y}) \) . \( n \) is the number of points used in the regression and \( \bar{x} \) is the mean of all the x values in the regression. s2 is the variance of the errors/residuals. Multiple Linear RegressionIn the case where the dependent Y-variable is dependent on more than one, say j, X-variables, we have the model: $$ Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \beta_3 X_3 + ... + \beta_j X_j + \epsilon $$A "point" in this model would then be a data set consisting of j + 1 numbers: $$ (y, x_1, x_2, x_3, ..., x_j) $$If we have \( i \) such "points" to be used in a multiple linear regression they can then be arranged as follows: $$ (y_1, x_{11}, x_{21}, x_{31}, ..., x_{j1}) $$ $$ (y_2, x_{12}, x_{22}, x_{32}, ..., x_{j2}) $$ $$ (y_3, x_{13}, x_{23}, x_{33}, ..., x_{j3}) $$ $$ ... $$ $$ (y_i, x_{1i}, x_{2i}, x_{3i}, ..., x_{ji}) $$The word "point" is here in quotations, because each of these data sets cannot be plotted as a dot in a coordinate system anyway, since we cannot draw things that has a dimension larger than 3. If the model has only 2 X-variables, that is; \( Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2\) we are able to plot the points (and the graph of the function) in a 3D coordinate system. The "linear" function Y will then be a plane in 3D. In general: if there are \( j \) X-variables in the model, the dimension of the model will be \( j + 1 \). The \( \beta_0 \) in the equation of the model is the intersection/intercept (or the "constant") and the other \( \beta \) values are the slopes belonging to their specific X variables. Each slope is the impact that its corresponding X variable has on the change of the Y variable. If for ex. the slope belonging to \( X_2 \) is \( \beta_2 = 0.34 \) then an increase in \( X_2 \) by 1 unit will lead to an increase in Y by 0.34 units, all other X variables remaining unchanged. A negative slope means that its corresponding X-variable has a negative effect on Y (an increase in this X will lead to a decrease in the Y value). If a \( \beta \) value is not significantly different from zero, this means that the corresponding X-variable does not have a significant impact/effect on the Y variable and this X-variable can therefore be omitted (ignored) in the model. To test whether a \( \beta \) value could be equal to zero (or any other value) one can perform a t-test with \( i - j - 1 \) degrees of freedom. If the p-value from the test is below the significance level (often 0.05) then we can reject the null hypothesis (H0) that says that \( \beta = 0 \) and the \( \beta \) is therefore significantly different from zero (or another chosen value). In order to find the beta values \( \beta_0, \beta_1, \beta_2, ..., \beta_j \) we can write the \( i \) equations, each equation corresponding to its specific point: $$ y_1 = \beta_0 + \beta_1 x_{11} + \beta_2 x_{21} + \beta_3 x_{31} + ... + \beta_j x_{j1} $$ $$ y_2 = \beta_0 + \beta_1 x_{12} + \beta_2 x_{22} + \beta_3 x_{32} + ... + \beta_j x_{j2} $$ $$ y_3 = \beta_0 + \beta_1 x_{13} + \beta_2 x_{23} + \beta_3 x_{33} + ... + \beta_j x_{j3} $$ $$ ... $$ $$ y_i = \beta_0 + \beta_1 x_{1i} + \beta_2 x_{2i} + \beta_3 x_{3i} + ... + \beta_j x_{ji} $$We must now find the set of \( \beta \) values that satisfy all of these equations simultaneously. This is impossible, however, since all the "points" do not lie on the same "line" in j + 1 dimensional space. We therefore introduce an error value \( \epsilon \) in each equation to make all the equations true. $$ y_1 = \beta_0 + \beta_1 x_{11} + \beta_2 x_{21} + \beta_3 x_{31} + ... + \beta_j x_{j1} + \epsilon_1 $$ $$ y_2 = \beta_0 + \beta_1 x_{12} + \beta_2 x_{22} + \beta_3 x_{32} + ... + \beta_j x_{j2} + \epsilon_2 $$ $$ y_3 = \beta_0 + \beta_1 x_{13} + \beta_2 x_{23} + \beta_3 x_{33} + ... + \beta_j x_{j3} + \epsilon_3 $$ $$ ... $$ $$ y_i = \beta_0 + \beta_1 x_{1i} + \beta_2 x_{2i} + \beta_3 x_{3i} + ... + \beta_j x_{ji} + \epsilon_i $$The task is now to find the smallest possible value of each of the \( \epsilon \) that will make the "line" get as close as possible to all the "points" at the same time. Written in matrix notation we get the set of equations to be $$ \begin{bmatrix} y_1 \\ y_2 \\ y_3 \\ ... \\ y_i \\ \end{bmatrix} = \begin{bmatrix} 1 & x_{11} & x_{21} & x_{31} & ... & x_{j1} \\ 1 & x_{12} & x_{22} & x_{32} & ... & x_{j2} \\ 1 & x_{13} & x_{23} & x_{33} & ... & x_{j3} \\ ... & ... & ... & ... & ... & ...\\ 1 & x_{1i} & x_{2i} & x_{3i} & ... & x_{ji} \\ \end{bmatrix} \cdot \begin{bmatrix} \beta_0 \\ \beta_1 \\ \beta_2 \\ ... \\ \beta_j \\ \end{bmatrix} + \begin{bmatrix} \epsilon_1 \\ \epsilon_2 \\ \epsilon_3 \\ ... \\ \epsilon_i \\ \end{bmatrix} $$Or (written in more compact matrix notation): $$ Y = X\beta + \epsilon $$Here, Y and \( \epsilon \) are \( i \cdot 1 \) column vectors. X is a \( i \cdot (j + 1) \) matrix and \( \beta \) is a \( (j + 1) \cdot 1 \) column vector. With the errors isolated we get: $$ Y - X\beta = \epsilon $$By squaring the errors we make sure they are always positive numbers: $$ \epsilon_i^2 = (y_i - \beta_0 - \beta_1 x_{1i} - \beta_2 x_{2i} - ... - \beta_j x_{ji})^2 $$The sum of all these squared errors $$ \sum_{k=1}^i{ (y_k - \beta_0 - \beta_1 x_{1k} - \beta_2 x_{2k} - ... - \beta_j x_{jk})^2 } $$must be as small as possible to make the "line" or "hyperplane" fit as good as possible to all the "points". It can be shown (eg. by use of differentiation) that this is achieved by setting $$ \beta = (X^T X)^{-1} (X^T X) Y $$XTX is the product of the X matrix with its own transposed matrix, XT. (XTX)-1 is the inverse of the XTX matrix. Having now found the \( \beta \) column with all the beta values of the model we can find the variance and the standard deviation of the errors: $$ s^2 = \frac{1}{i - j - 1} \sum_{k=1}^i{\epsilon_k^2} \iff s = \sqrt{\frac{1}{i - j - 1} \sum_{k=1}^i{\epsilon_k^2}} $$The standard deviations of each of the \( \beta \) values are now found as the square roots of the diagonal elements in the matrix: $$ s^2 \cdot (X^T X)^{-1} $$After having found the \( \beta \) values, an F-test can be performed to test the null hypothesis H0: all the slopes are equal to zero; \( \beta_1 = \beta_2 = \beta_3 = ... = \beta_j = 0 \). In other words; the overall value of the model is useless, since none of the X variables contribute significantly to the change in the Y values. This is held up against the alternative hypothesis H1: at least one of the slopes is different from zero. The F value for the test is calculated as $$ F = \frac{R^2 / j}{(1 - R^2)/(i - j - 1)} $$The corresponding p value is then found as described under F-test in chapter "means" with degrees of freedom DF1 = j and DF2 = i - j - 1 . For a given set of x-values \( (x_1, x_2, x_3, ..., x_j) \) we can calculate the corresponding expected (or predicted) y-value according to the model: $$ \hat{y} = \beta_0 + \beta_1 \cdot x_1 + \beta_2 \cdot x_2 + \beta_3 \cdot x_3 + ... + \beta_j \cdot x_j $$This will then be the value that y should have, to make the "point" \( (\hat{y}, x_1, x_2, x_3, ..., x_j) \) lie directly on the "line" or "hyperplane" of the model. A confidence interval of this \( \hat{y} \) can be calculated as: $$ CI = \hat{y} \; \pm \; t_{(1-\frac{\alpha}{2})} \cdot SE_{\hat{y}} $$The number \( t_{(1-\frac{\alpha}{2})} \) is the \( (1-\frac{\alpha}{2})\cdot 100 \% \) quantile of the t-distribution with (i - j - 1) degrees of freedom and significance level α. See section "t-test" in chapter "means" above for further info. \( SE_{\hat{y}} \) is the standard error of \( \hat{y} \) . It can be found the following way: $$ SE_{\hat{y}} = \sqrt{ s^2 (1 + X_0^T(X^T X)^{-1} X_0) } $$Here, \( X_0 \) is the \( (1+j) \cdot 1 \) dimensional row vector \( (1,x_1,x_2,x_3,...,x_j)\). \( X_0^T \) is the transposed of this vector (written vertically instead of horizontically). s2 is the variance of the errors/residuals and \( (X^T X)^{-1} \) is the inverse of \( X^T X \) (see above). The above formula for \( SE_{\hat{y}} \) holds in general for all cases. If, however, the number of variables is only 1, i.e. the model is: \( Y = \beta_0 + \beta_1 X_1 \) the following formula could also be used instead: $$ SE_{\hat{y}} = \sqrt{ s^2 \left( 1 + \frac{1}{i} + \frac{ (x - \bar{x})^2 }{\sum_{k=1}^i{x_k^2} - i\bar{x}^2} \right)} $$Where x is the x-value from the point \( (x, \hat{y}) \) satisfying \( \hat{y} = \beta_0 + \beta_1 \cdot x \) . \( i \) is the number of points used in the regression and \( \bar{x} \) is the mean of the x values. Correlation MatrixThe correlation between two data sets X1 and X2 of equal size is a number between -1 and 1. It is used to decide whether the two data sets can or cannot be assumed independent from each other. If the correlation is close to -1 or 1 the data sets are strongly correlated. If the correlation is close to 0 they are uncorrelated. In a multivariable linear regression model, all the X variables X1, X2, ... Xk should be independent from one another. Meaning that for any pair of two X data sets, Xi and Xj, their correlation should be 0 or close to zero for the linear regression model to be valid. In other words \( corr(X_i , X_j) = 0 \) . In contrast, the correlation between the Y variable and any one of the X variables should be strong, i.e. close to -1 or 1. Formula for correlation between Xi and Xj: $$ corr(X_i , X_j) = \frac{ Mean(X_i \cdot X_j) - Mean(X_i) \cdot Mean(X_j) }{ \sqrt{ Mean(X_i^2) - Mean(X_i)^2} \cdot \sqrt{ Mean(X_j^2) - Mean(X_j)^2} } $$ $$ = \frac{ \overline{X_i X_j} - \overline{X_i} \cdot \overline{X_j} }{ \sqrt{ \overline{X_i^2} - \overline{X_i}^2} \cdot \sqrt{ \overline{X_j^2} - \overline{X_j}^2} } $$The correlation matrix contains the correlation coefficients between any two of the involved samples or data sets. The matrix is symmetric, since \( corr(X_i , X_j) = corr(X_j , X_i)\). Singular Logistic RegressionIf we have a dependent Y variable, which is binary, i.e. that can only take the values 0 and 1, the value y=1 could represent the patient having the disease and the value y=0 could represent the opposite (the patient not having the disease),then we want a function p(x) that only gives output values between 0 and 1, namely the probability that a certain patient has the disease, given the input data of that patient. For eg. (in the case of singular logistic regression) if a patient with the x-value 23.56 has the disease/outcome the function p should give p(23.56) = 1 (or a number as close to 1 as possible). The logistic function will fulfill these criteria: $$ p(x) = \frac{1}{1 + \text{e}^{-(\beta_0 + \beta_1 x)}} , $$where the values of the parameters β0 and β1 must be chosen so that the function value p(x) will predict the correct outcome as precisely as possible: If a patient has the disease, then p(x) should be as close to 1 as possible, if a patient doesn't have the disease p(x) should be as close to 0 as possible, noticing that p(x) can never be precisely 1 or 0. Example: If we have the following data sets for Y and X: $$ Y = [0,0,0,0,0,0,1,0,1,1] $$ $$ X = [1,2,3,4,5,6,7,8,9,10] , $$we want to find the values of β0 and β1 that makes the function predict the actual Y-values as precisely as possibly given the X-values. Using logistic regression we find that β0 = -9.5270 and β1 = 1.2675. The function p(x) will then be: $$ p(x) = \frac{1}{1 + \text{e}^{-(-9.5270 + 1.2675 x)}} $$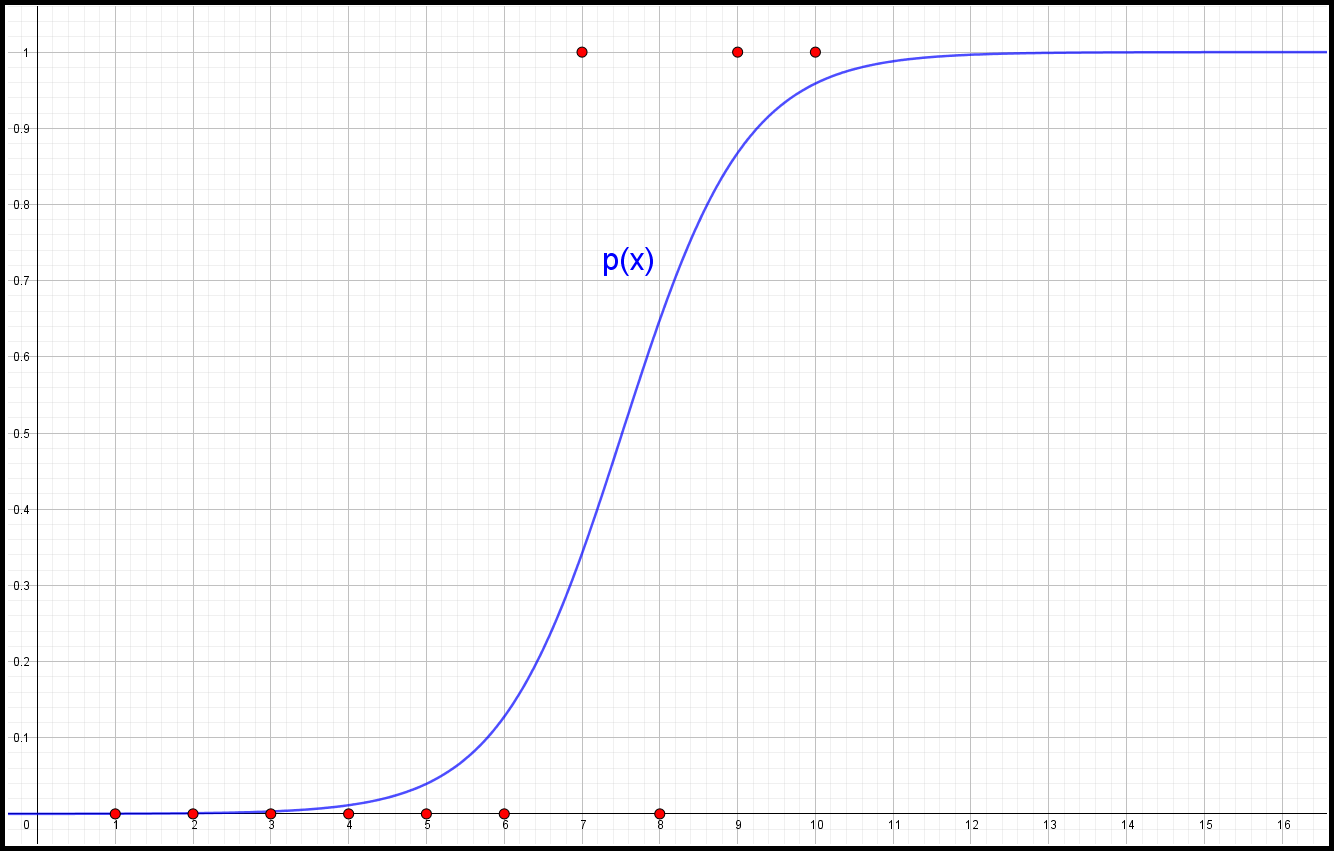
In this example p(10) = 0.9588 . This number is not exactly 1 (as it should have been, since the corresponding y-value to x = 10 is 1), but it's the closest it can get with the beta values found, which are the most optimal. Instead of using probability/risk p(x) one can translate into odds: $$ odds = \frac{p(x)}{1 - p(x)} = \text{e}^{\beta_0 + \beta_1 x} = \text{e}^{\beta_0} \times \text{e}^{\beta_1 x} = baseline \times OR^x $$Using odds instead of risk can be an advantage in many cases, for eg. risk is a limited number which can only have values between 0 and 1. The methods used for finding the most optimal values of the beta values, which will make the curve get as
close as possible to all the points at the same time, are complicated.
The task is then to find the optimal values of the betas which will make the likelihood as large as possible. Since a product of numbers between 0 and 1 will approach 0 quite fast, it's more convenient to work with the "log likelihood" instead, by taking the natural logarithm on both sides of the above equation: $$ \ln(LLH) = y_1 \ln(p(x_1)) + (1 - y_1) \ln(1 - p(x_1)) + y_2 \ln(p(x_2)) + (1 - y_2) \ln(1 - p(x_2)) + ... $$ $$ ... + y_n \ln (p(x_n)) + (1 - y_n) \ln(1 - p(x_n)) $$This won't give problems, since a maximum of the likelihood in terms of the betas will also be a maximum of the log likelihood. The maximizing method itself is an algorithm involving Newton-Rhapson's formula of finding an extremum. Multiple Logistic RegressionIf there's more than one independent X variable, the principles and methods are the same as in the case of simple logistic regression above; we still need to find the set of beta values (β0, β1, ..., βn), that will maximize the likelihood of the model: $$ p(x) = \frac{1}{1 + \text{e}^{-(\beta_0 + \beta_1 x_1 + \beta_2 x_2 + ... + \beta_n x_n)}} $$For example, if there are the three following X variables: blood pressure (X1), weight (X2) and age (X3) with the following values:
And y=1 being disease/outcome and y=0 not disease, then a logistic regression will give the following values:
Written into the equation of p(x): $$ p(x) = \frac{1}{1 + \text{e}^{-(-8.5165 + 0.0744 x_1 + 0.0455 x_2 - 0.0305 x_3)}} $$Written in the Odds Ratio notation: $$ Odds = 0.0002 \times 1.0772^{x_1} \times 1.0465^{x_2} \times 0.9700^{x_3} $$Interpretation of the OR values: In a logistic regression, the variables involved will be adjusted for the confounding effect (if any), that the other variables have on it. In other words the OR value of 1.0772 means that for every increase of 1 in blood pressure, the odds of getting the outcome/disease will be 1.0772 times higher, everything else being the same, after having adjusted for the confounding effects of weight (X2) and age (X3). Power & Sample Size
Calculate power or sample size HERE. Both in the dichotomous case as well as the continuous case.
Power1. Dichotomous Outcome (proportions): To calculate the power (1 - β) of a study given the proportions p1 and p2 and sample sizes n1 and n2 you can isolate the number \( z_{(1 - \beta)} \) in the below formula for n1 under sample size, which gives: $$ z_{(1 - \beta)} = \frac{ \sqrt{n_1(p_2 - p_1)^2} - z_{(1-\frac{\alpha}{2})} \sqrt{\left( 1 + \frac{1}{r} \right) \left( \frac{p_1 + p_2 \cdot r}{1 + r} \right) \left( 1 - \frac{p_1 + p_2 \cdot r}{1 + r} \right) } }{ \sqrt{p_1 (1 - p_1) + p_2 \left( \frac{1 - p_2}{r} \right) } } $$\( z_{(1-\frac{\alpha}{2})} \) is the z-value corresponding to the \( 1-\frac{\alpha}{2} \) percentile in the standard normal distribution. For ex. if α = 0.05 then \( z_{(1-\frac{\alpha}{2})} = z_{(1-\frac{0.05}{2})} = z_{0.975} = 1.96 \) Then the power (1 - β) is found as the area under the normal distribution function from \( -\infty \) to \( z_{(1 - \beta) } \) $$ 1 - \beta = \int_{-\infty}^{z_{(1 - \beta) }} \frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2} \cdot x^2} dx $$2. Continuous Outcome (mean values): To calculate the power (1 - β) of a study given the mean values \( \bar{x}_1 \) and \( \bar{x}_2 \), sample sizes n1, n2 plus the common SD: $$ 1 - \beta = \int_{-\infty}^{z_A} \frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2} \cdot x^2} dx + \int_{-\infty}^{z_B} \frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2} \cdot x^2} dx $$ $$ \text{where } z_A = z - z_{(1-\frac{\alpha}{2})} \text{ and } z_B = -z - z_{(1-\frac{\alpha}{2})} $$\( z_{(1-\frac{\alpha}{2})} \) is the z-value corresponding to the \( 1-\frac{\alpha}{2} \) percentile in the standard normal distribution. For ex. if α = 0.05 then \( z_{(1-\frac{\alpha}{2})} = z_{(1-\frac{0.05}{2})} = z_{0.975} = 1.96 \) The number \( z \) is found in this way: $$ z = \frac{\bar{x}_1 - \bar{x}_2}{SD\sqrt{\frac{1}{n_1} + \frac{1}{n_2}}} $$Sample Size1. Dichotomous Outcome (proportions): To calculate the minimum necessary sample sizes n1 and n2 of a study given the proportions p1 and p2, the power 1 - β and the ratio \( r = \frac{n_2}{n_1} \): $$ n_1 = \frac{ \left( z_{(1-\frac{\alpha}{2})} \sqrt{\left( 1 + \frac{1}{r} \right)\left( \frac{p_1 + p_2 \cdot r}{1 + r} \right)\left( 1 - \frac{p_1 + p_2 \cdot r}{1 + r} \right)} + z_{(1-\beta)} \sqrt{p_1 (1 - p_1) + p_2 \frac{1 - p_2}{r}} \right)^2 }{(p_2 - p_1)^2} $$ $$ n_2 = r \cdot n_2 $$\( z_{(1-\frac{\alpha}{2})} \) is the z-value corresponding to the \( 1-\frac{\alpha}{2} \) percentile in the standard normal distribution. For ex. if α = 0.05 then \( z_{(1-\frac{\alpha}{2})} = z_{(1-\frac{0.05}{2})} = z_{0.975} = 1.96 \) Same with \( z_{(1 - \beta)} \); it's the z-value corresponding to the \( 1 - \beta \) percentile in the standard normal distribution. For ex. if β = 0.80 then \( z_{(1 - \beta)} = z_{(1 - 0.80)} = z_{0.2} = 0.842 \) 2. Continuous Outcome (mean values): To calculate the minimum necessary sample sizes n1 and n2 of a study given the means \( \bar{x}_1 , \bar{x}_2 \), the common SD, the power 1-β and the ratio \( r = \frac{n_2}{n_1} \): $$ n_1 = \left( 1 + \frac{1}{r} \right) \cdot \left(SD \cdot \frac{ z_{(1-\frac{\alpha}{2})} + z_{(1-\beta)}}{\bar{x}_2 - \bar{x}_1}\right)^2 $$ $$ n_2 = r \cdot n_1 $$\( z_{(1-\frac{\alpha}{2})} \) and \( z_{(1 - \beta)} \) : see above. Survival Analysis
Do survival analysis HERE. Calculate life tables, life curves and Kaplan-Meier curves and estimates plus log-rank test.
Survival estimates and survival curvesIn survival analysis one or more risk groups are followed over time to see if they develop an outcome. The
outcome in this case is often death, but cut also be, more generally expressed, failure. If patients in the study do not fail/die, they
can be "censored" instead, either when they withdraw from the study (while it's still in progress) or are still alive at the time of study
termination. The later type of censoring is called right censoring in contrast to left censoring, which occurs when the patient is censored
before study start. Most common censoring is right censoring and the "time" for a right censored patient is then amount of time the patient
has survived in the study until censoring occurs. The status "censored" is marked with the number 0 and "death/failure" with the number 1.
In the table, the patient with ID A145 belonged to the placebo group, survived for 6 weeks and then died,
whereas the patient with ID B141 belonged to the treatment group, survived for 9 weeks and then got censored.
In the above life tables, the number at risk in each time period is obtained by subtracting half of the
censored patients in the time period from the patients alive at the start of the period. Assuming that the censored were censored on average
half way through the time period. The number alive at the start of each period is obtained by subtracting the number of deaths and censored
during the previous period. The survivor function Si is the probability of surviving through this time period i (and longer),
given that one has survived up until then. It's obtained by multiplying the initial Si with all subsequent si, For
eg. in group 2, the chance of surviving 9 weeks (or more) is S = 1 × 0.8333 × 0.7778 = 0.6481.
The sums in the expression of se are over all time periods (rows) in the above table up until and including the particular time ti. After the calculation of the life tables for each of the groups, the survival curve of the survivor function
S(i) can be drawn by connecting the dots ( ti, S(i) ) with lines, where the ti's are the times in the life table and
the S(i)'s are the probabilities of the survivor function.
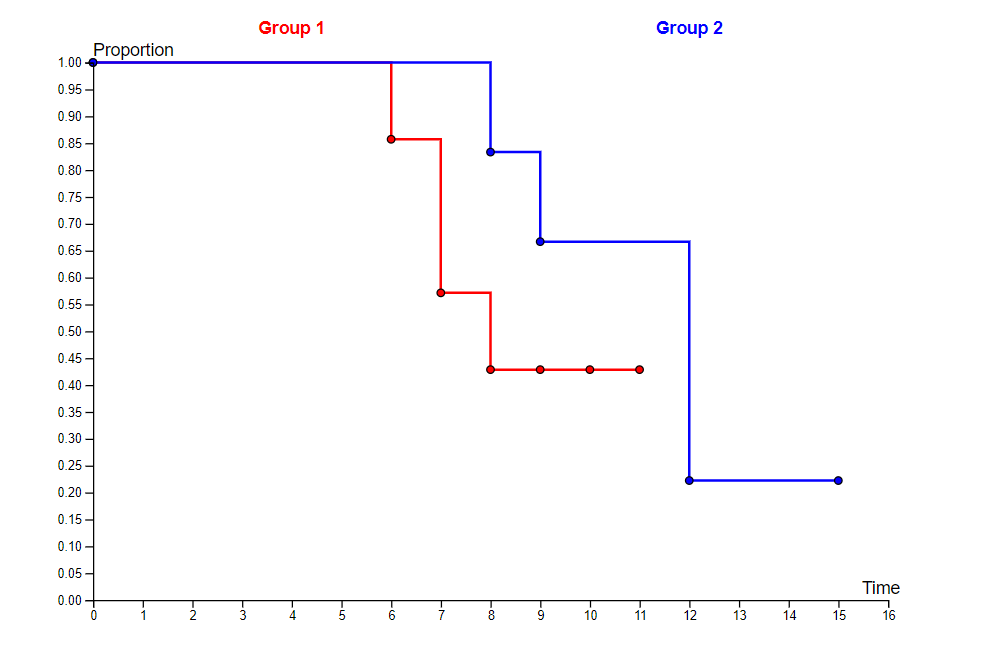
Kaplan-Meier estimates and Kaplan-Meier curvesThe Kaplan-Meier estimate for each group involved in the study is calculated using the following procedure:
Here, the number at risk at each time period is obtained by subtracting all dead and censored at the previous
time. The probabilities of the survivor function S(t) for a specific time t is obtained like in the above method of the life tables by
multiplying the value of S(t) from the previous time by the probability of surviving the current time period S(t) = S(tprevious)
× s(t).
Mantel-Cox hazard ratio estimateBetween two groups involved in a study (for eg. treatment vs. placebo) it's possible to calculate the Mantel-Cox hazard ration estimate. The ratio between the two rates are calculated under the assumption that each rate is constant during the entire period of time. And that the curves of the survivor functions of the two groups don't cross each other, i.e. one is constantly above the other. The calculation of the Mantel-Cox estimate of the hazard ratio is done with this formula: $$ HR_{MC} = \frac{Q}{R} , \text{ where } Q = \sum_{j=1}^J { \frac{d_{1j} \times h_{0j}}{n_j} } \text{ and } R = \sum_{j=1}^J { \frac{d_{0j} \times h_{1j}}{n_j} } $$In the formula, J is the total number of distinct days (or weeks or months ... ) in the study (the
no. of rows in the above table) and j is the index of each specific time in the left table column, for eg. t = 7 which would have
index j = 3. h0j is the number of patients that survived the time period j in the first group, d1j is
the amount who died during time period j in the second group and vice versa with h1j and d0j.
nj is the total amount of patients at risk in both groups at start of time j.
In the formula, dj is the sum of the dead in both groups at each specific time j. n1j and n0j are the no. of patients at risk in group 1 and 0 respectively at start of time j. Log-rank test of equality between the rates of two groupsIt can be tested whether the hazard rates, and hence the survival rates, of two groups can be assumed to be equal. This is done with the Mantel-Cox chi-square test, also known as the log-rank test. It is (as the name indicates) a chi-square (χ2) test where the observed numbers of deaths in the groups are compared with the expected numbers of deaths in the groups, if the rates had been the same in the groups. The chi-square number is calculated as follows: $$ \chi^2 = \frac{U^2}{V} , \text{ where } U = \sum_{j=1}^J {\left( d_{1j} - \frac{d_j \times n_{1j}}{n_j} \right) } $$The corresponding p-value is then obtained from the chi-square-distribution as the area under the curve of the chi-square probability density function from χ2 to infinity. If the p-value is below 0.05 we can reject the null hypothesis, saying that the rates of the two groups are equal. In this case the rates are then significantly different from each other on a 5% significance level. The degrees of freedom (DF) in this case is always 1 (since there are two groups). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||