Get p-values for probability density functions from data input

Tables

Decimals:

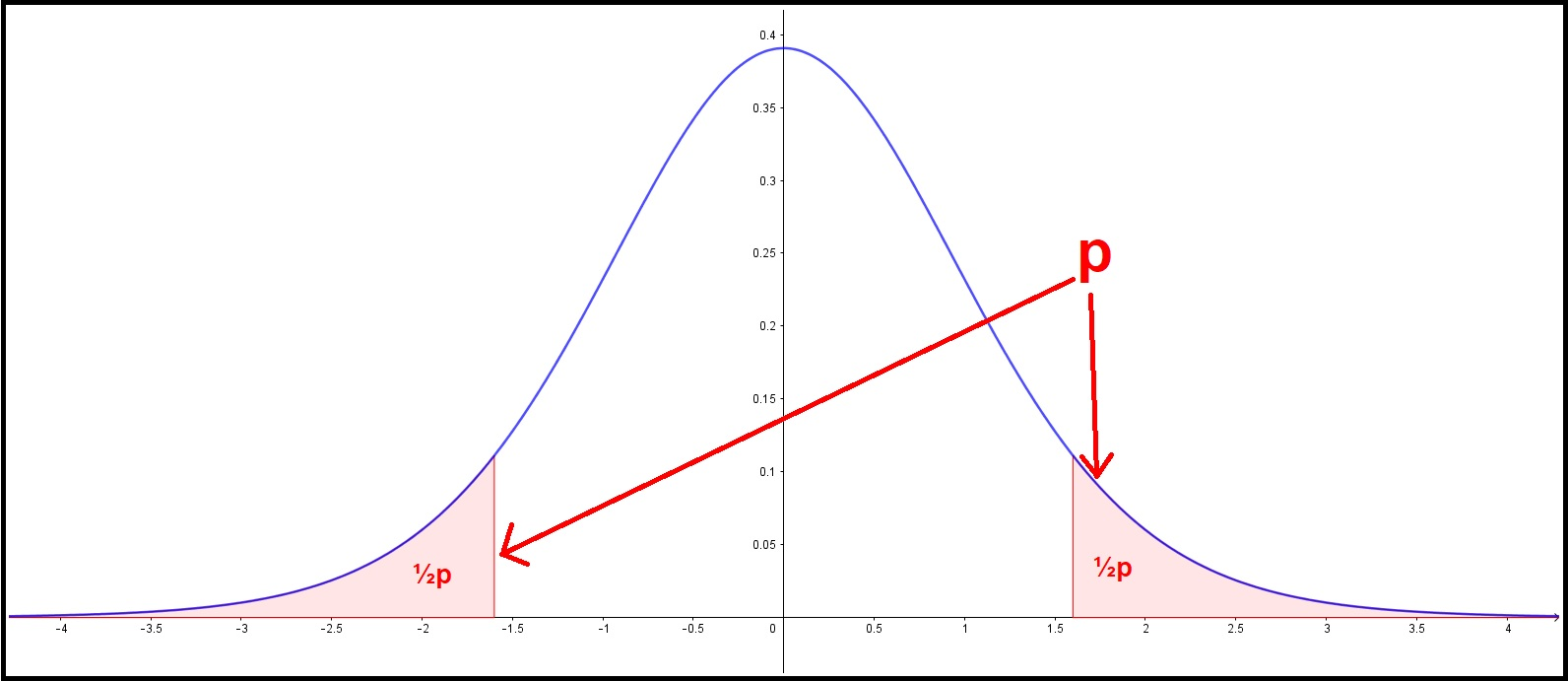
The Standard Normal Distribution: $ N(0,1) $

The z-value and the p-value to be entered in the table below are defined to satisfy the following:

$$ p = 2 \ \cdot P(Z > |z|) = 2 \ \cdot \int_{|z|}^{\infty} \phi(z) \: dz $$

Where $ \phi(z) $ is the standard normal distribution with mean 0 and standard deviation 1:

$$ \phi(z) = \frac{1}{\sqrt{2\pi}} \ \cdot \text{e}^{-\frac{1}{2} z^2} $$

In other words: the p-value is two times the area under the bell shaped curve from |z| to infinity. The number |z| is the numerical (positive) value of z. If, for example, the z-value is z = -1.43, then the number to be entered into the table is |z| = |-1.43| = 1.43. And if z = 2.27, then |z| = |2.27| = 2.27.

For example:

$$ 0.05 = 2 \ \cdot 0.025 = 2 \ \cdot P(Z > |1.96|) = 2 \ \cdot \int_{1.96}^{\infty} \phi(z) \: dz $$

The p-value is the two-sided (or two-tailed) area under the bell curve; one area from each "tail". The two areas are the same, since the function is symmetric. If you only need (or only have) half of the p-value, the table can still be used; just enter the |z| value and get the p and ½p values. Or enter either p or ½p to get the other two values.

Picture of both tails in the two-sided p-value of the cumulative normal distribution function

Enter either |z|, p or $ \frac{1}{2} $p to get the other two
Standard Normal distribution X ~ N(0, 1) table
\|z\|	p (two-sided)	$ \frac{1}{2} $p (one-sided)

The Normal Distribution: $ X \text{~} N(μ , σ) $

If you have a general normal distribution with mean μ and standard deviation σ, and need the area under the bell shaped curve from x₁ to x₂ then the p value is defined as follows:

$$ p = P(x_1 < X < x_2) = P(X < x_2) - P(X < x_1) = \int_{x_1}^{x_2} f(x) \: dx $$

Where $ f(x) $ is (in this case) the normal distribution with mean μ and standard deviation σ :

$$ f(x) = \frac{1}{\sqrt{2\pi \sigma^2}} \ \cdot \text{e}^{-\frac{(x - \mu)^2}{2 \sigma^2}} $$

If you need the lower bound to be minus infinity ( $-\infty$ ) or the upper bound to be infinity ($ \infty $), in other words if you need one of the following areas;

$$ p = \int_{-\infty}^{x_2} f(x) \: dx \:\: \color{blue}{\text{or}} \:\: \color{black}{p = \int_{x_1}^{\infty} f(x) \: dx} $$

then you can type either "-INF" as the x₁ value or "INF" as the x₂ value.

Picture of the area under the curve between two x values in the cumulative normal distribution function

Two of the four inputs **must** be μ and σ in order to get the fifth value
Normal distribution X ~ N(μ, σ) table
Mean (μ)	SD (σ)	x₁	x₂	p-value

The F Distribution

An f-test is performed to test whether the variances of two samples can be assumed equal. In other words whether the null hypothesis is rejected or not rejected. The null hypothesis states that H0: Var₁ = Var₂ , where Var₁ = (SD₁)² is the variance of the first sample and Var₂ = (SD₂)² is the variance of the second sample. Consequently, $ SD_1 = \sqrt{Var_1} = \sqrt{(SD_1)^2}$ is the standard deviation of the first sample. And $ SD_2 = \sqrt{Var_2} = \sqrt{(SD_2)^2}$ is the standard deviation of the second sample involved in the f-test. Another way of stating the H0 hypothesis is that the ratio of the variances is 1:

$$ H_0 : \frac{(SD_1)^2}{(SD_2)^2} = 1 \:\: \text{(or)} \:\: H_0 : \frac{(SD_2)^2}{(SD_1)^2} = 1 $$

The f₁-value, the f₂ value and the corresponding p₁ and p₂ values are defined as follows:

$$ f_1 = \frac{(SD_1)^2}{(SD_2)^2} , f_2 = \frac{(SD_2)^2}{(SD_1)^2} = \frac{1}{f_1} $$

The number p₁ is the smallest of the two following numbers:

$$ p = \int_{f_1}^\infty{f(x)} \: dx \: \: \: \: \: \: \text{and} \:\:\:\:\:\: 1-p $$

The number p₂ is the smallest of the two following numbers:

$$ p = \int_{f_2}^\infty f(x) \: dx \:\:\:\:\:\: \text{and} \:\:\:\:\:\: 1-p $$

The overall p-value in an F-test, taking into consideration both f₁ and f₂, is therefore the following number:

$$ p_{total} = p_1 + p_2 $$

The f-test starts by assuming that H0 is in fact true, namely that Var₁ = Var₂. The overall p-value p_total (a number between 0 and 1) is the probability of getting as big a deviation from the hypothetical f-value of 1, or an even bigger deviation, as the one being observed. For the start assumption was that H0 is true; meaning that both f-values should be equal to 1, or at least close to 1, in correspondance with the assumption.

If the overall p-value (p_total) is below the significance level (typically five percent i.e. α = 0.05) then the null hypothesis is rejected, and the two variances are therefore significantly different from each other, because then it's extremely unlikely to get that big a deviation from what would be expected, given the initial assumption that H0 is true.

The function $ f(x) $ is the probability density function of the F-distribution defined as:

$$ f(x) = \frac{df_1^{\frac{df_1}{2}} \cdot df_2 ^\frac{df_2}{2} \cdot \Gamma\left(\frac{df_1 + df_2}{2}\right) \cdot x^{\frac{df_1}{2}-1}}{\Gamma\left(\frac{df_1}{2}\right) \cdot \Gamma\left(\frac{df_2}{2}\right) \cdot \left(df_2 + df_1 \cdot x\right)^{\frac{df_1 + df_2}{2}}} , $$

where DF₁ = N₁ - 1 is the degree of freedom of the first sample and DF₂ = N₂ - 1 is the degree of freedom of the second sample. For more details, go to page "Formulas" in the menu.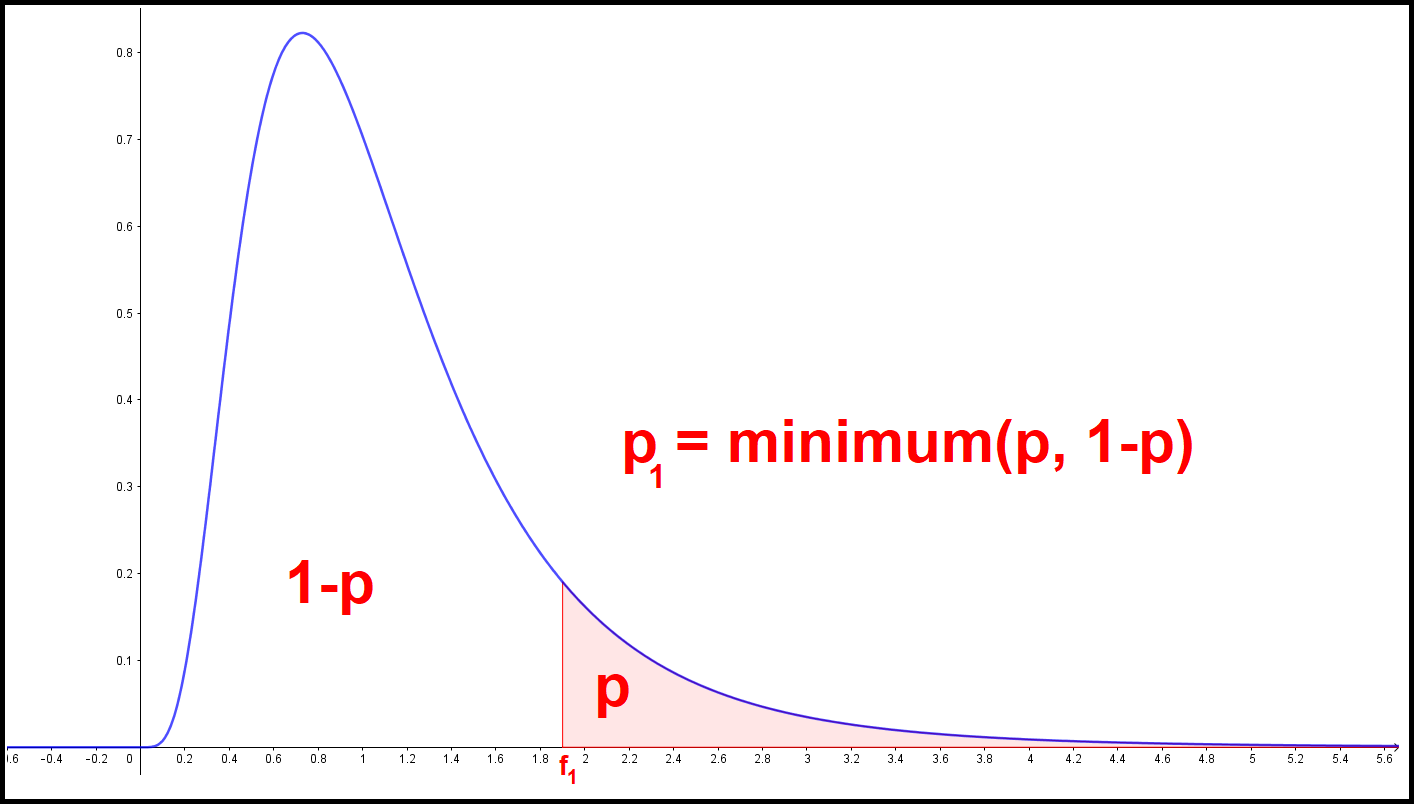

Picture showing the area under the curve together with the complement p-value of the cumulative F distribution function from an f value to infinity

Use the following table if you have the standard deviations SD₁ and SD₂ from the two samples:

Enter the four inputs SD₁, SD₂, DF₁ and DF₂ to get the remaining five
F-distribution table in the case of known standard deviations
SD₁	SD₂	DF₁	DF₂	f₁	f₂	p₁	p₂	p_total

Use the following table if you have the variances Var₁ = (SD₁)² and Var₂ = (SD₂)² from the two samples:

Enter the four inputs (SD₁)², (SD₂)², DF₁ and DF₂ to get the remaining five
F-distribution table in the case of known variances
(SD₁)²	(SD₂)²	DF₁	DF₂	f₁	f₂	p₁	p₂	p_total

*****************************************************************************************************************************

If you only need to find a specific p-value corresponding to a particular f-value (or the other way around), in other words an f and a p value satisfying that

$$ p = P(X > f) = \int_{f}^\infty{f(x)} \: dx , $$

you can then instead use the table below over f-distribution values given DF₁ and DF₂ and either p or f:

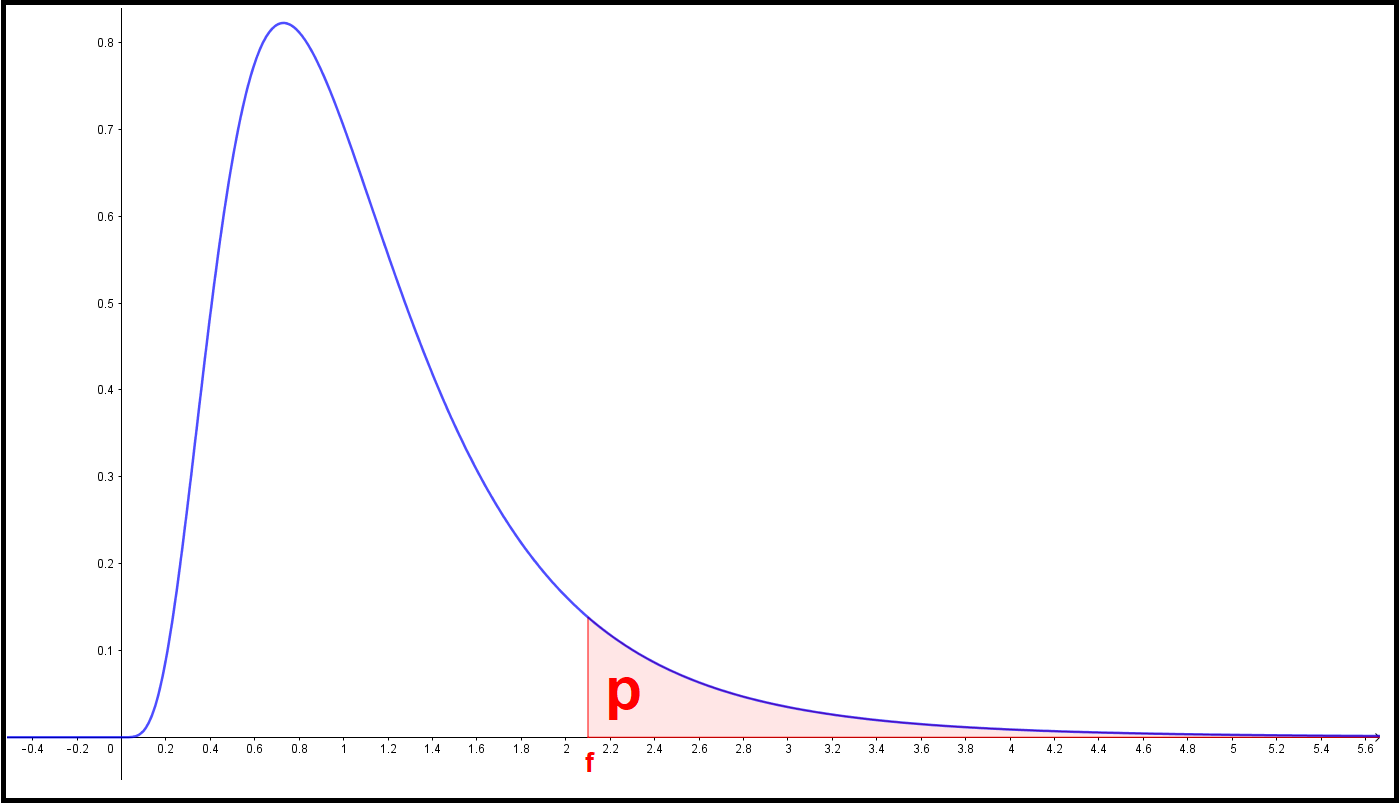
Picture of the area under the curve of the cumulative F distribution function from an f value to infinity

Two of the three inputs MUST be DF₁ and DF₂ in order to get the fourth.
F-distribution table
DF₁	DF₂	f	p

The T-Distribution

The |t|-value, the DF-number and the corresponding p-value are defined as follows:

$$ p = 2 \ \cdot P(T > |t|) = 2 \ \cdot \int_{|t|}^{\infty} f(x) \: dx , $$

where $ f(x) $ is the probability density function of the T-distribution with DF degrees of freedom:

$$ f(x) = \frac{\Gamma{\left( \frac{df+1}{2}\right)}}{\sqrt{\pi \cdot df} \cdot \Gamma{\left(\frac{df}{2}\right)} \cdot \left( 1 + \frac{x^2}{df}\right)^{(df+1)/2}} $$

|t| is the numerical (positive) value of the t-value.

You can input either the two-sided (two-tailed) p-value in order to get the |t| value and the one-sided ½p value. Or you can input the one-sided ½p value and get the |t| value and the p-value. Or input the |t| value and get p as well as ½p.

For more details, go to the page "Formulas" in the menu.

Picture of both tails by a two-sided p-value under the curve of the cumulative t distribution function

One of the two inputs MUST be DF in order to get the remaining two values
T-distribution table
t-value	DF	p (two-sided)	$ \frac{1}{2} $ p (one-sided)

*****************************************************************************************************************************

If you are looking for the areal under the bell curve of the probability density function of the T-Distribution between two t-values t₁ and t₂, you can use the table below instead:

The p-value will then be the integral:

$$ p = P(t_1 < T < t_2) = \int_{t_1}^{t_2} f(x) \: dx , $$

where $ f(x) $ is the probability density function of the T-distribution with DF degrees of freedom (see above)

If t₁ is $-\infty$ (minus infinity) you can write "-inf" as input under t₁.

If t₂ is $\infty$ (infinity) you can write "inf" as input under t₂.

The p-values would then in those cases be:

$$ p = P(-\infty < T < t_2) = \int_{-\infty}^{t_2} f(x) \: dx \:\: \color{blue}{\text{or}} \:\: \color{black}{p = P( t_1 < T < \infty) = \int_{t_1}^{\infty} f(x) \: dx} $$
Picture of the p-value as the area under the curve between two t values of the cumulative t distribution function

Picture of the p-value as the area under the curve between two t values of the cumulative t distribution function

One of the three inputs MUST be DF in order to get the fourth
T-Distribution table
DF	t₁	t₂	p-value

The Chi-Square-Distribution ($\chi^2$)

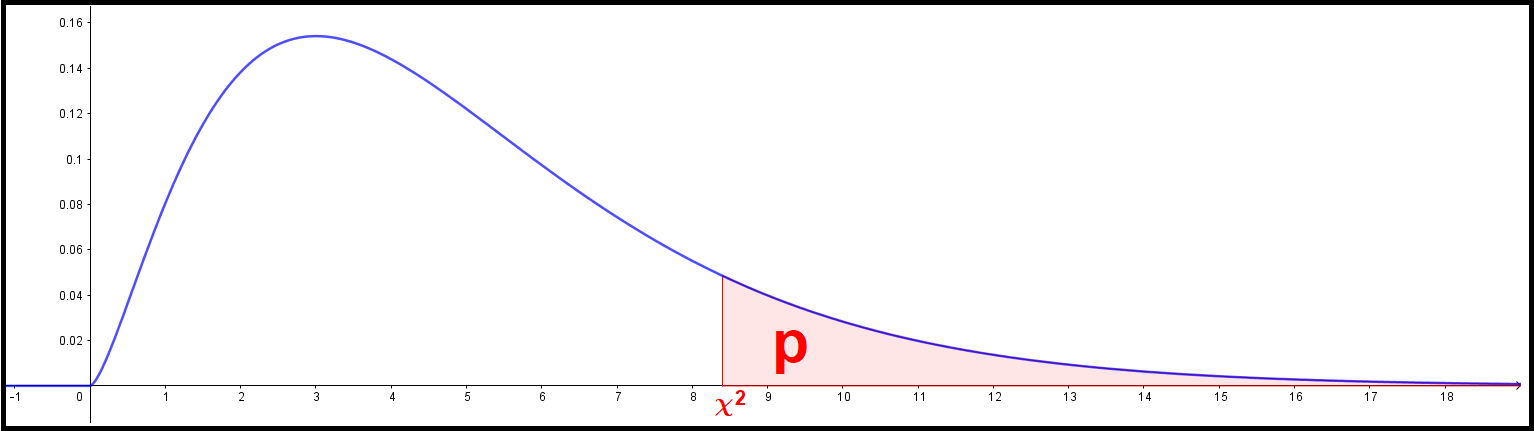
The χ² - value, the DF-number and the corresponding p-value are defined as follows:

$$ p = P(X > \chi^2) = \int_{ \chi^2 }^{\infty} f(x) \: dx , $$

where $ f(x) $ is the probability density function of the chi-square-distribution with DF degrees of freedom:

$$ f(x) = \frac{x^{\frac{1}{2} \cdot df - 1} \cdot \text{e}^{-\frac{1}{2} \cdot x}}{2^{\frac{1}{2} \cdot df} \cdot \Gamma\left( \frac{df}{2}\right)} $$

In other words the p-value is the area under the curve from χ² to infinity. For more details, go to the page "Formulas" in the menu.

Picture of the p-value as the area under the curve from a chi value to infinity of the cumulative chi distribution function

One of the two inputs MUST be DF to get the third
Chi-Square-Distribution table
$ \chi^2 $ value	DF	p-value

Tables

The z-value and the p-value to be entered in the table below are defined to satisfy the following:

Where \( \phi(z) \) is the standard normal distribution with mean 0 and standard deviation 1:

For example:

If you have a general normal distribution with mean μ and standard deviation σ, and need the area under the bell shaped curve from x₁ to x₂ then the p value is defined as follows:

Where \( f(x) \) is (in this case) the normal distribution with mean μ and standard deviation σ :

If you need the lower bound to be minus infinity ( \(-\infty\) ) or the upper bound to be infinity (\( \infty \)), in other words if you need one of the following areas;

then you can type either "-INF" as the x₁ value or "INF" as the x₂ value.

The f₁-value, the f₂ value and the corresponding p₁ and p₂ values are defined as follows:

The number p₁ is the smallest of the two following numbers:

The number p₂ is the smallest of the two following numbers:

The overall p-value in an F-test, taking into consideration both f₁ and f₂, is therefore the following number:

The function \( f(x) \) is the probability density function of the F-distribution defined as:

where DF₁ = N₁ - 1 is the degree of freedom of the first sample and DF₂ = N₂ - 1 is the degree of freedom of the second sample. For more details, go to page "Formulas" in the menu.

Use the following table if you have the standard deviations SD₁ and SD₂ from the two samples:

Use the following table if you have the variances Var₁ = (SD₁)² and Var₂ = (SD₂)² from the two samples:

*****************************************************************************************************************************

If you only need to find a specific p-value corresponding to a particular f-value (or the other way around), in other words an f and a p value satisfying that

you can then instead use the table below over f-distribution values given DF₁ and DF₂ and either p or f:

The |t|-value, the DF-number and the corresponding p-value are defined as follows:

where \( f(x) \) is the probability density function of the T-distribution with DF degrees of freedom:

*****************************************************************************************************************************

If you are looking for the areal under the bell curve of the probability density function of the T-Distribution between two t-values t₁ and t₂, you can use the table below instead:

The p-value will then be the integral:

where \( f(x) \) is the probability density function of the T-distribution with DF degrees of freedom (see above)

If t₁ is \(-\infty\) (minus infinity) you can write "-inf" as input under t₁.

If t₂ is \(\infty\) (infinity) you can write "inf" as input under t₂.

The p-values would then in those cases be:

The χ² - value, the DF-number and the corresponding p-value are defined as follows:

where \( f(x) \) is the probability density function of the chi-square-distribution with DF degrees of freedom:

In other words the p-value is the area under the curve from χ² to infinity. For more details, go to the page "Formulas" in the menu.

The z-value and the p-value to be entered in the table below are defined to satisfy the following:

Where \( \phi(z) \) is the standard normal distribution with mean 0 and standard deviation 1:

For example:

If you have a general normal distribution with mean μ and standard deviation σ, and need the area under the bell shaped curve from x1 to x2 then the p value is defined as follows:

Where \( f(x) \) is (in this case) the normal distribution with mean μ and standard deviation σ :

If you need the lower bound to be minus infinity ( \(-\infty\) ) or the upper bound to be infinity (\( \infty \)), in other words if you need one of the following areas;

then you can type either "-INF" as the x1 value or "INF" as the x2 value.

The f1-value, the f2 value and the corresponding p1 and p2 values are defined as follows:

The number p1 is the smallest of the two following numbers:

The number p2 is the smallest of the two following numbers:

The overall p-value in an F-test, taking into consideration both f1 and f2, is therefore the following number:

The function \( f(x) \) is the probability density function of the F-distribution defined as:

where DF1 = N1 - 1 is the degree of freedom of the first sample and DF2 = N2 - 1 is the degree of freedom of the second sample. For more details, go to page "Formulas" in the menu.

Use the following table if you have the standard deviations SD1 and SD2 from the two samples:

Use the following table if you have the variances Var1 = (SD1)2 and Var2 = (SD2)2 from the two samples:

*****************************************************************************************************************************

If you only need to find a specific p-value corresponding to a particular f-value (or the other way around), in other words an f and a p value satisfying that

you can then instead use the table below over f-distribution values given DF1 and DF2 and either p or f:

The |t|-value, the DF-number and the corresponding p-value are defined as follows:

where \( f(x) \) is the probability density function of the T-distribution with DF degrees of freedom:

*****************************************************************************************************************************

If you are looking for the areal under the bell curve of the probability density function of the T-Distribution between two t-values t1 and t2, you can use the table below instead:

The p-value will then be the integral:

where \( f(x) \) is the probability density function of the T-distribution with DF degrees of freedom (see above)

If t1 is \(-\infty\) (minus infinity) you can write "-inf" as input under t1.

If t2 is \(\infty\) (infinity) you can write "inf" as input under t2.

The p-values would then in those cases be:

The χ2 - value, the DF-number and the corresponding p-value are defined as follows:

where \( f(x) \) is the probability density function of the chi-square-distribution with DF degrees of freedom:

In other words the p-value is the area under the curve from χ2 to infinity. For more details, go to the page "Formulas" in the menu.

If you have a general normal distribution with mean μ and standard deviation σ, and need the area under the bell shaped curve from x₁ to x₂ then the p value is defined as follows:

then you can type either "-INF" as the x₁ value or "INF" as the x₂ value.

The f₁-value, the f₂ value and the corresponding p₁ and p₂ values are defined as follows:

The number p₁ is the smallest of the two following numbers:

The number p₂ is the smallest of the two following numbers:

The overall p-value in an F-test, taking into consideration both f₁ and f₂, is therefore the following number:

where DF₁ = N₁ - 1 is the degree of freedom of the first sample and DF₂ = N₂ - 1 is the degree of freedom of the second sample. For more details, go to page "Formulas" in the menu.

Use the following table if you have the standard deviations SD₁ and SD₂ from the two samples:

Use the following table if you have the variances Var₁ = (SD₁)² and Var₂ = (SD₂)² from the two samples:

you can then instead use the table below over f-distribution values given DF₁ and DF₂ and either p or f:

If you are looking for the areal under the bell curve of the probability density function of the T-Distribution between two t-values t₁ and t₂, you can use the table below instead:

If t₁ is \(-\infty\) (minus infinity) you can write "-inf" as input under t₁.

If t₂ is \(\infty\) (infinity) you can write "inf" as input under t₂.

The χ² - value, the DF-number and the corresponding p-value are defined as follows:

In other words the p-value is the area under the curve from χ² to infinity. For more details, go to the page "Formulas" in the menu.